Python算法学习笔记
[TOC]
绪论
数据结构
数据的两种结构逻辑结构和存储结构(物理结构)
- 逻辑结构
- 线性结构
- 线性表
- 队列
- 栈
- 非线性结构
- 树形结构
- 图状结构
- 集合结构
- 线性结构
- 存储结构
- 顺序存储结构
- 链式存储结构
算法
算法是解决某一特定问题的指定描述
算法的特征
- 有穷性
- 确定性(唯一性)
- 可行性
- 输入
- 输出
算法的评价
- 正确性
- 可读性
- 健壮性
- 效率和低存储
算法的时间复杂度
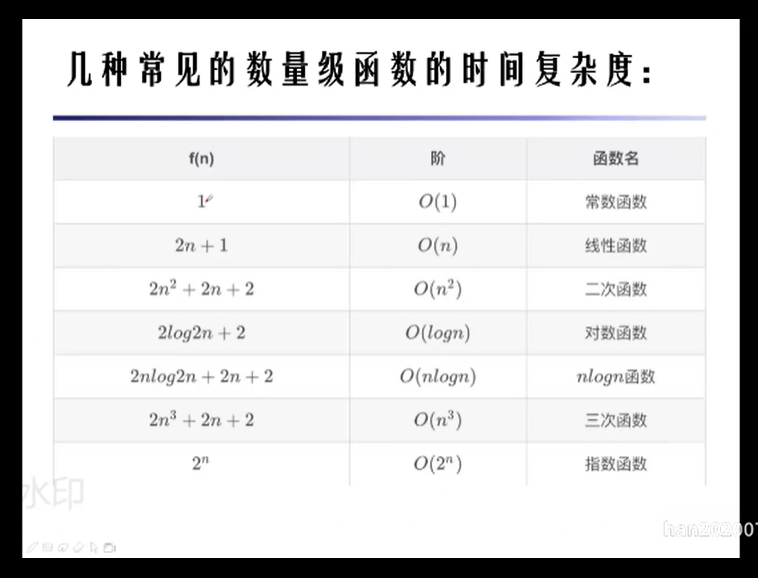
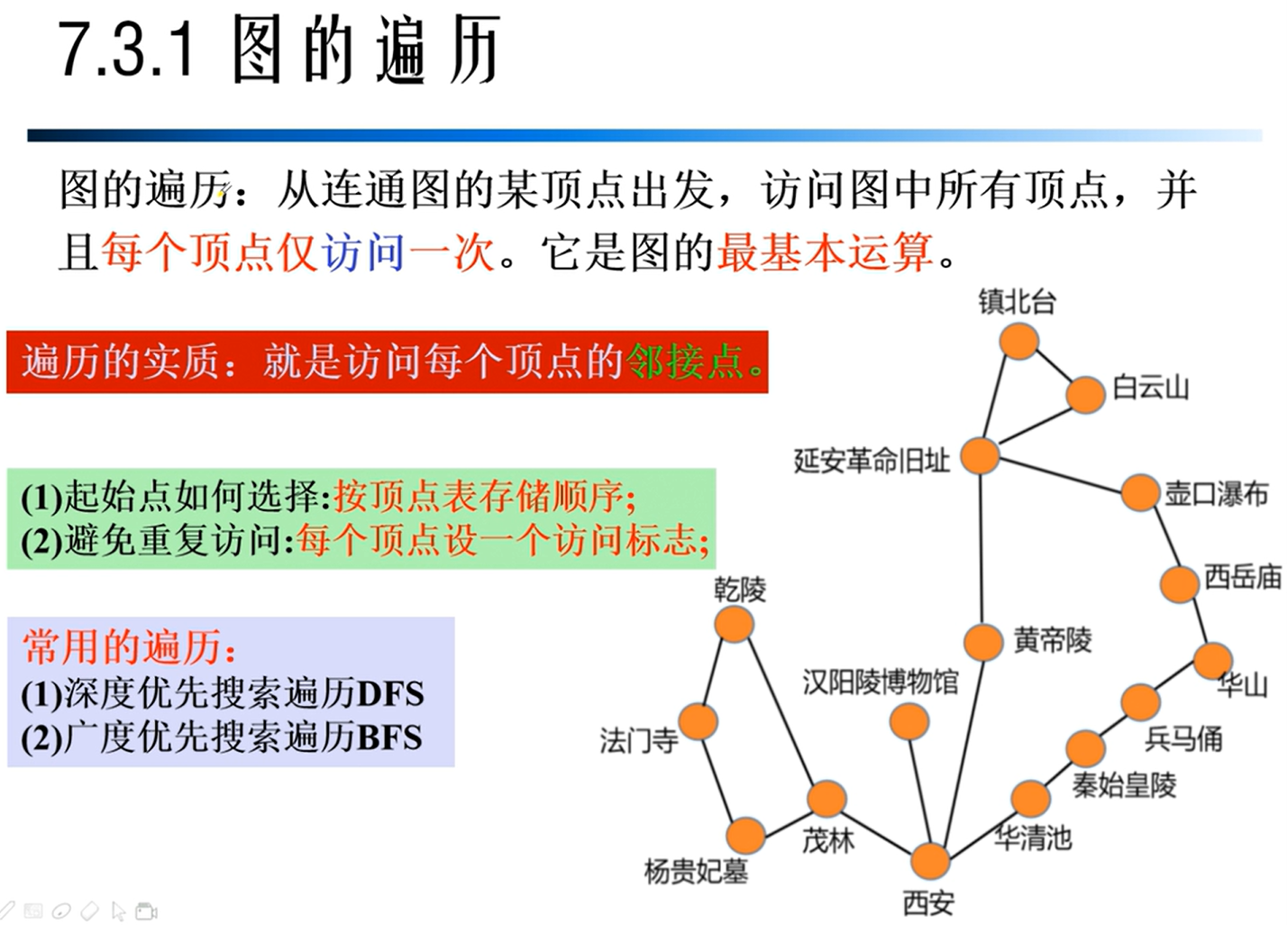
算法的空间复杂度
和时间复杂度相比不那么重要,一般算法采取的措施为用空间换时间,即用一部分的空间消耗来缩短计算时间。
递归
汉诺塔问题(递归调用)
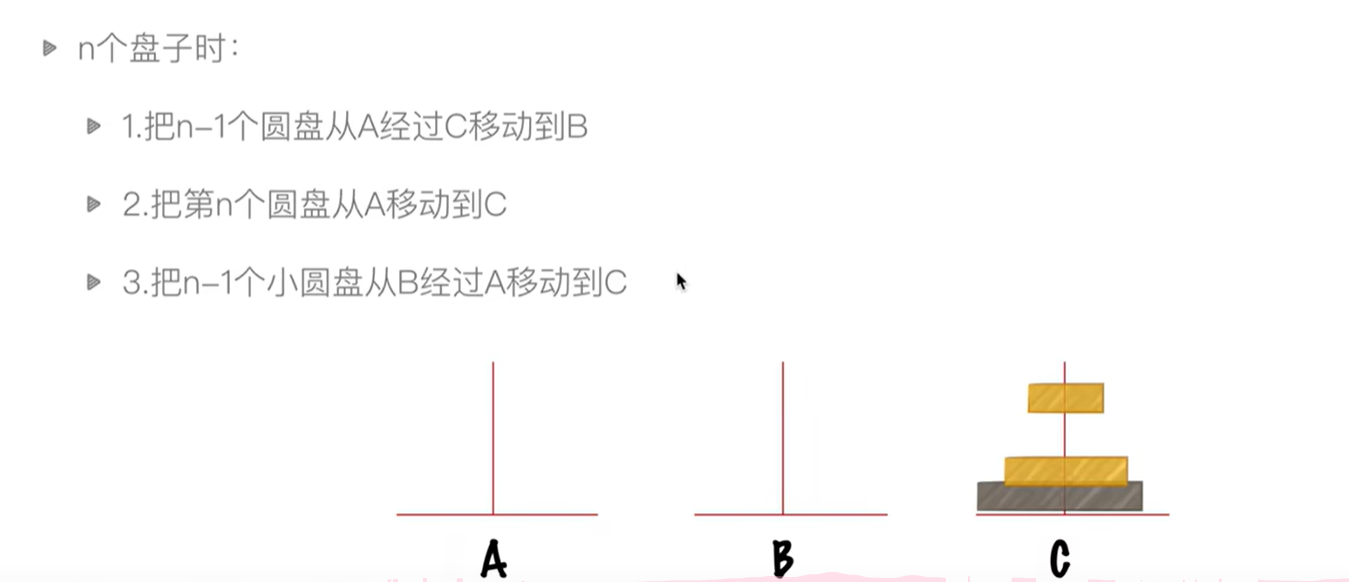
1 | # 汉诺塔算法 |
查找排序
二分查找
1 | # 二分查找 |
检查排序是否完成
1 | def check(li, reverse=False): |
冒泡排序
1 | # 冒泡排序 |
选择排序
1 | # 选择排序 |
插入排序
1 | # 插入排序 |
希尔排序(高级版插入排序)
1 | # 希尔排序 |
快速排序
1 | # 快速排序 |
堆排序(二叉树)
1 | # 堆排序 |
python中内置好的堆排序函数
1 | # python中内置好的堆排序 |
利用堆排序解决topk问题
1 | # 利用堆排序解决topk问题 |
归并排序
1 | # 归并排序 |
六种排序方法的总结
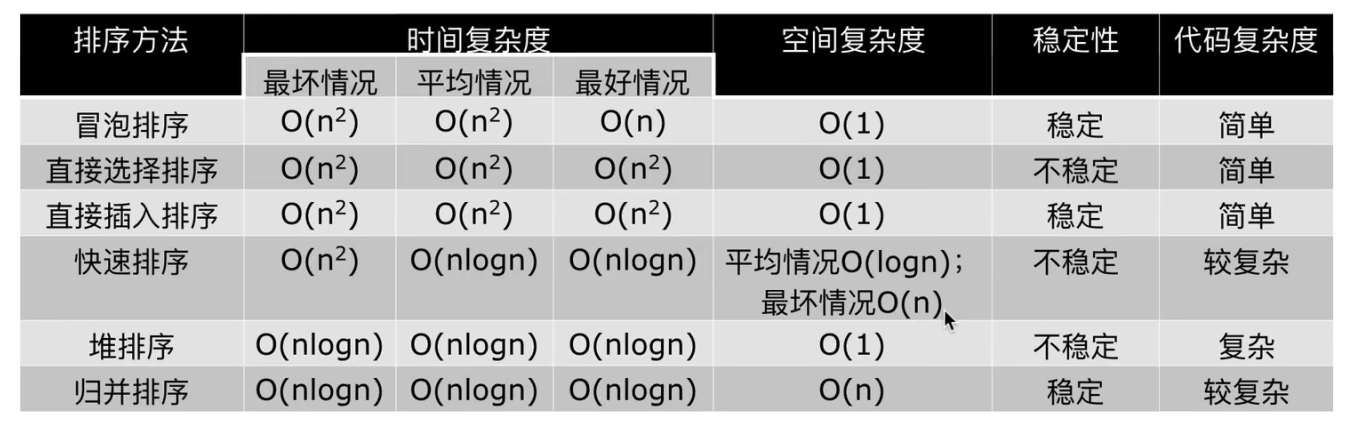
计数排序
1 | # 计数排序 |
桶排序(高级版计数排序)
1 | # 桶排序 |
基数排序
1 | # 基数排序 |
数据结构
线性表
列表(即顺序表)
- 列表内的每个节点储存的元素为地址,所以列表内部可以时任意数据类型
- 列表是动态分配存储空间,列表长度不够的时候,python底层会为列表重新开辟一个更大的空间,并把原先列表中存储的地址复制到新开辟的空间中
栈(后进先出)
顺序栈
列表(li)结构可以实现栈
- 进栈:li.append
- 出栈:li.pop
- 取栈顶:li[-1]
1 | class Stack: |
链式栈
1 | class stack_linked(): |
栈的应用
迷宫问题(找的不一定是最短路径)
1 | map = [ |
十进制转化为其他进制
1 | # 十进制转化为其他进制 |
队列(先进先出)
列表(li)可以实现队列
- 入队:li.append
- 出队:li.pop(0)
- 取队头:li[0]
顺序队列
基础队列类
1 | class Queue: |
循环队列类
1 | class Queue: |
内置队列
1 | from collections import deque # 双向队列 |
链式队列
1 | class Node(): |
队列的应用
迷宫问题(求的是最短路径)
1 | map = [ |
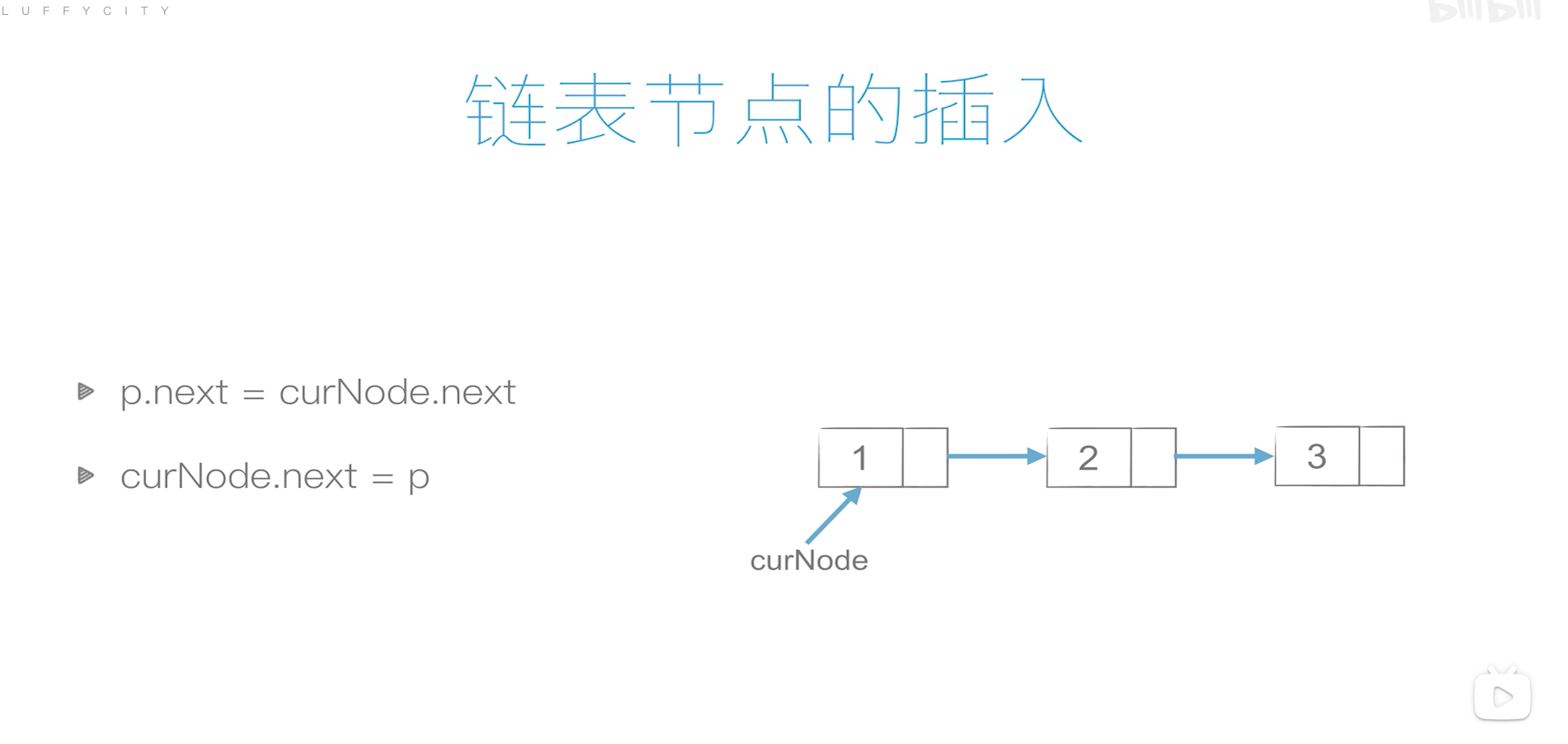
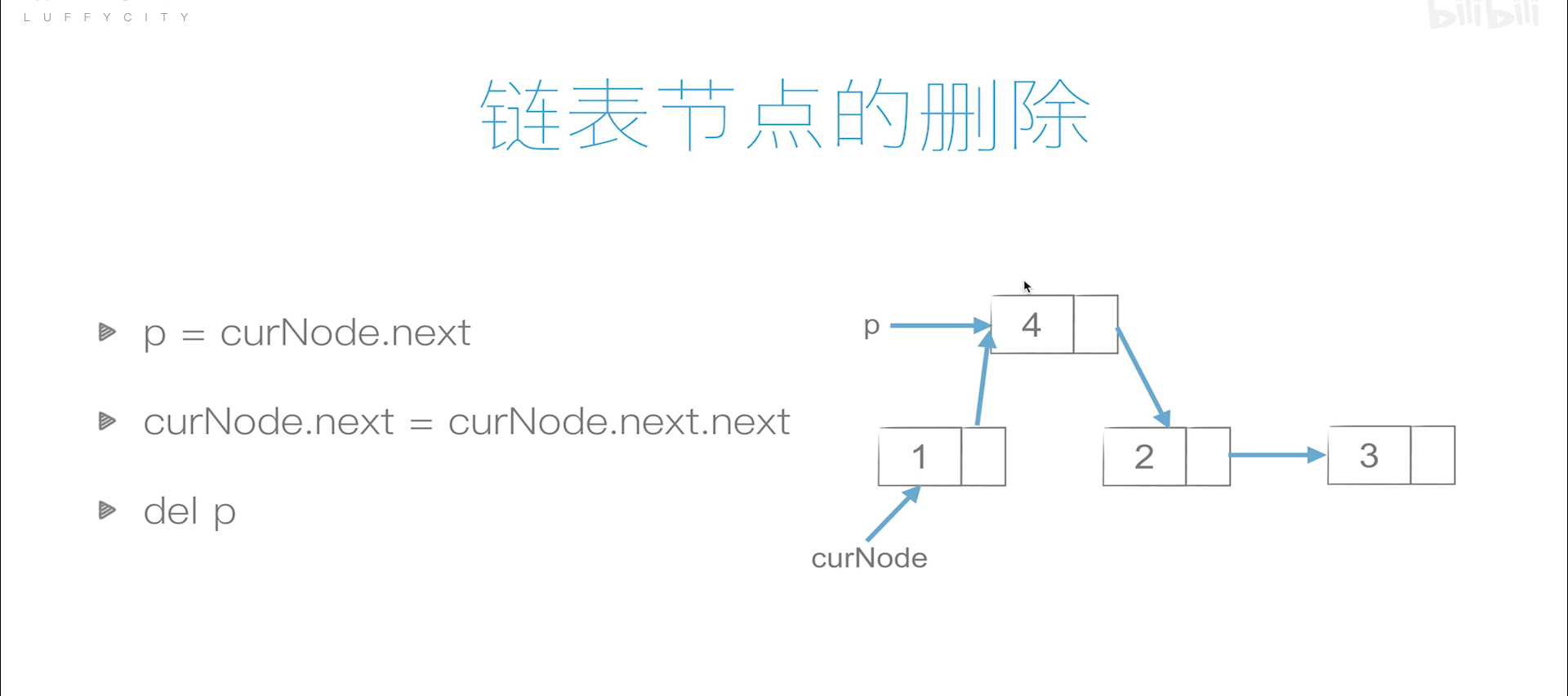
链表
单链表
单链表的创建
1 | class ListNode: |
1 | class ListNode: |
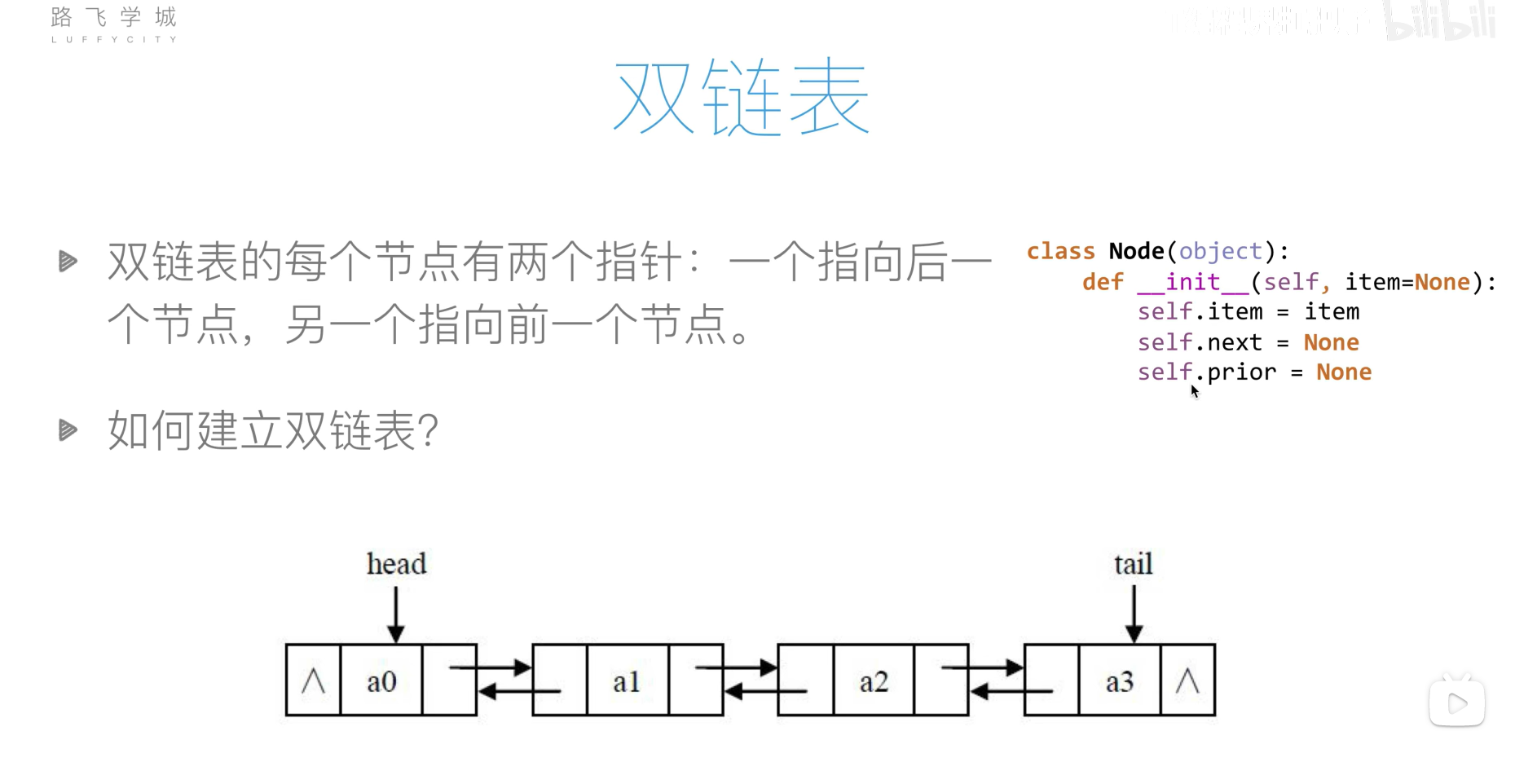
双链表
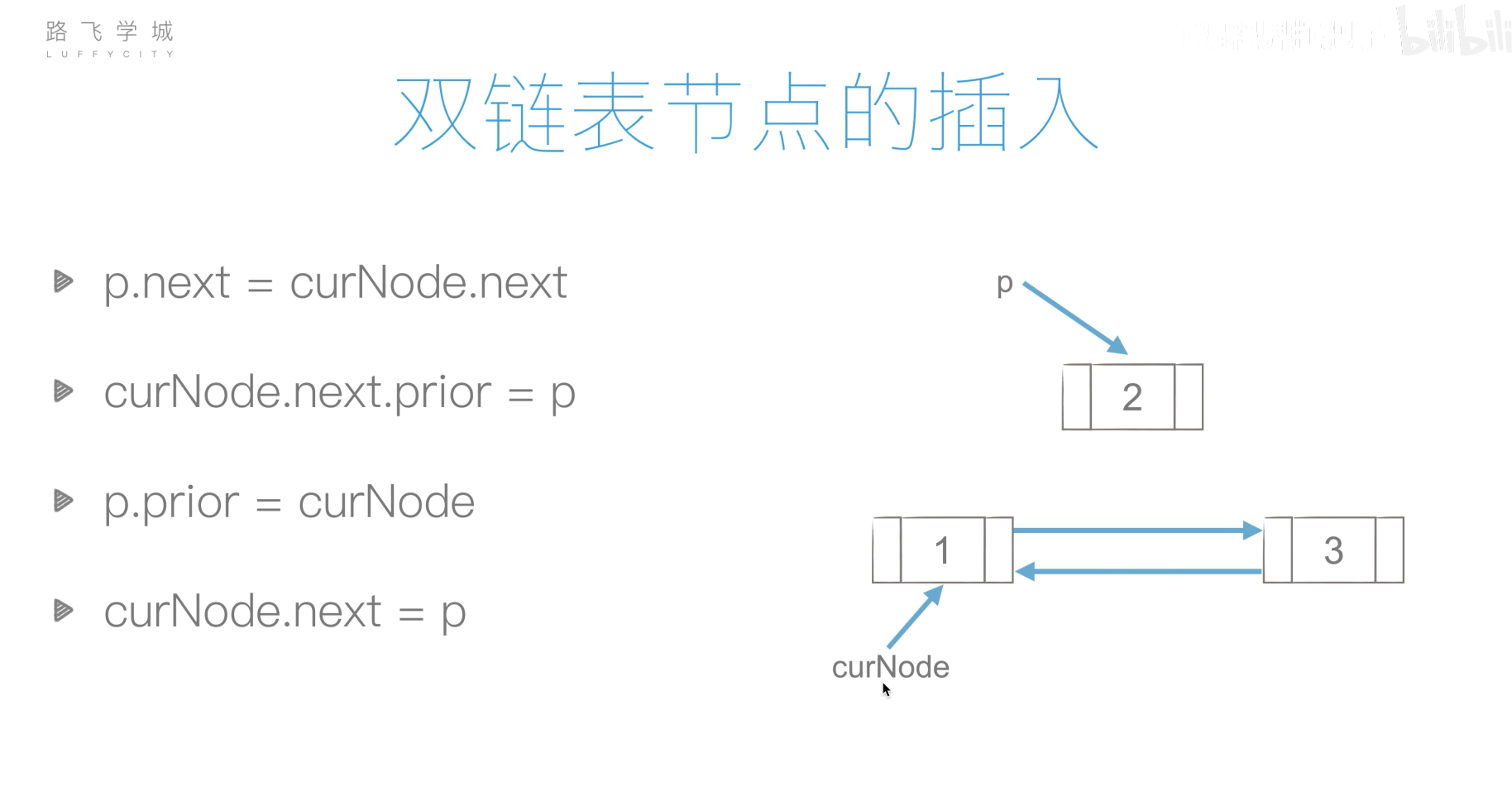
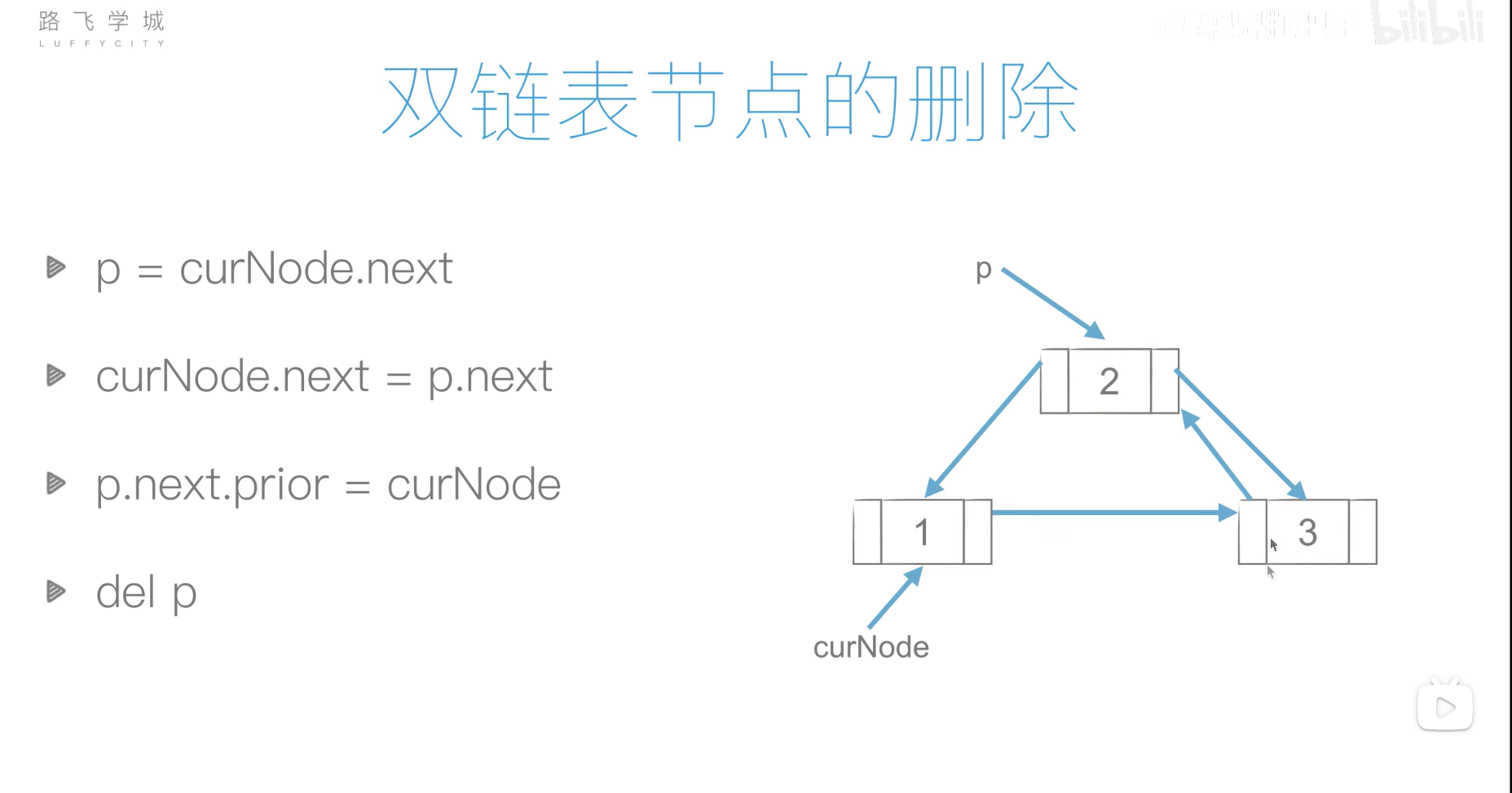
双链表的创建
1 | class Node: |
链表与数组的差别
- 链表
- 优点:插入删除操作较快,内存可以动态分配
- 缺点:查找操作较慢
- 数组
- 优点:结构简单,查找操作快
- 缺点:插入删除操作较慢,内存不能动态分配
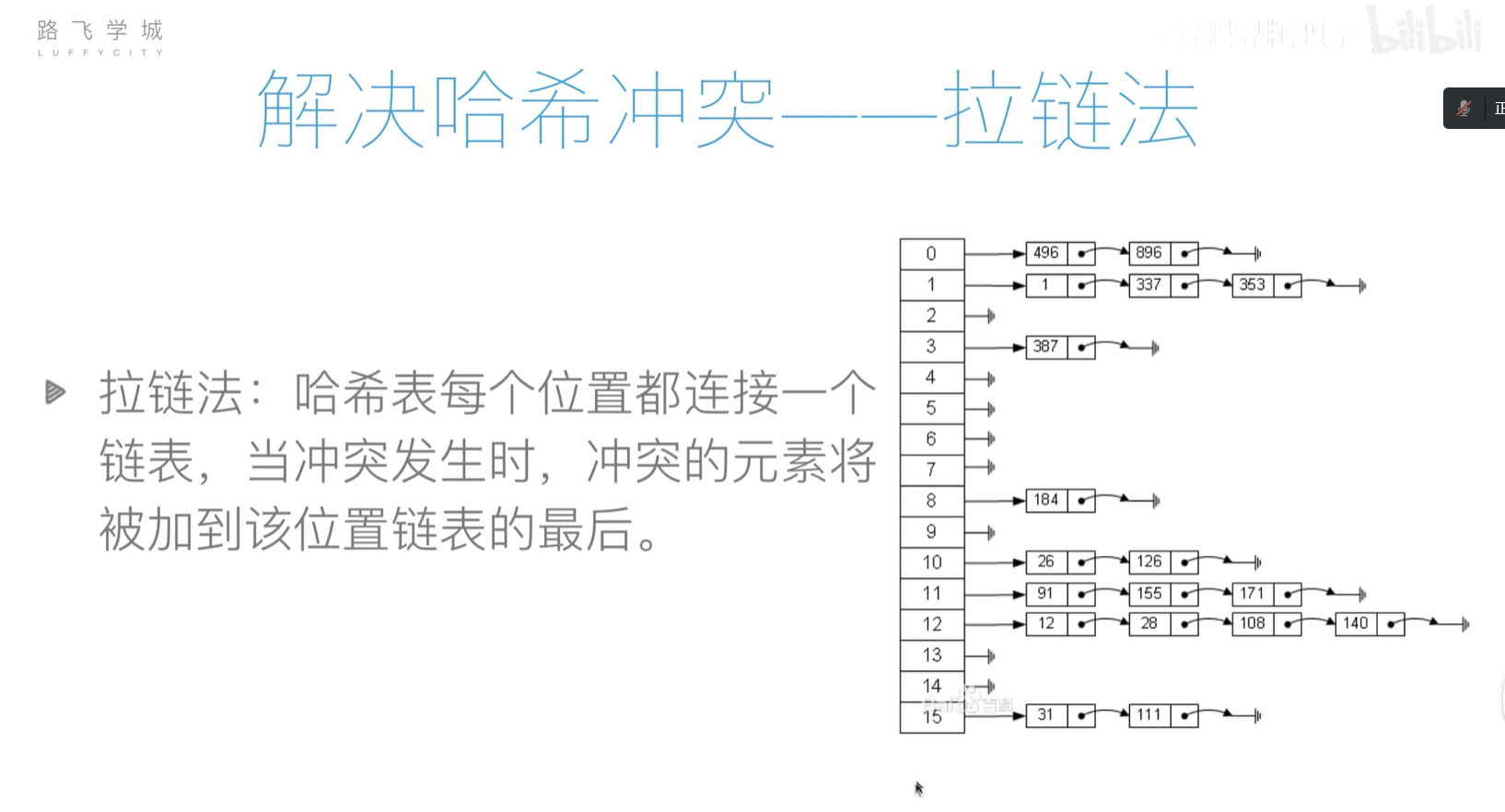
哈希表
python中的集合,字典结构在底层都是用的哈希表来实现的
哈希表(开辟的一系列连续的地址即数组)
哈希函数(计算输入的值在哈希表中对应下标的函数)
哈希冲突(对于不同的输入哈希函数输出的结果可能相同)
- 解决哈希冲突的方法
- 线性探测法:如果地址冲突,那么它所存放的位置在哈希表中加一
- 二次探测法:利用二次函数,计算冲突时,应该存储的位置
- 拉链存储法:哈希表的每个节点存储的是链表
树和二叉树
基本概念
- 根节点
- 叶子节点
- 树的深度
- 节点的度
- 树的度
- 父亲节点
- 孩子节点(左孩子/右孩子)
- 子树
二叉树(度为2的树)
二叉树的性质
对于非空二叉树,如果叶子节点树为n
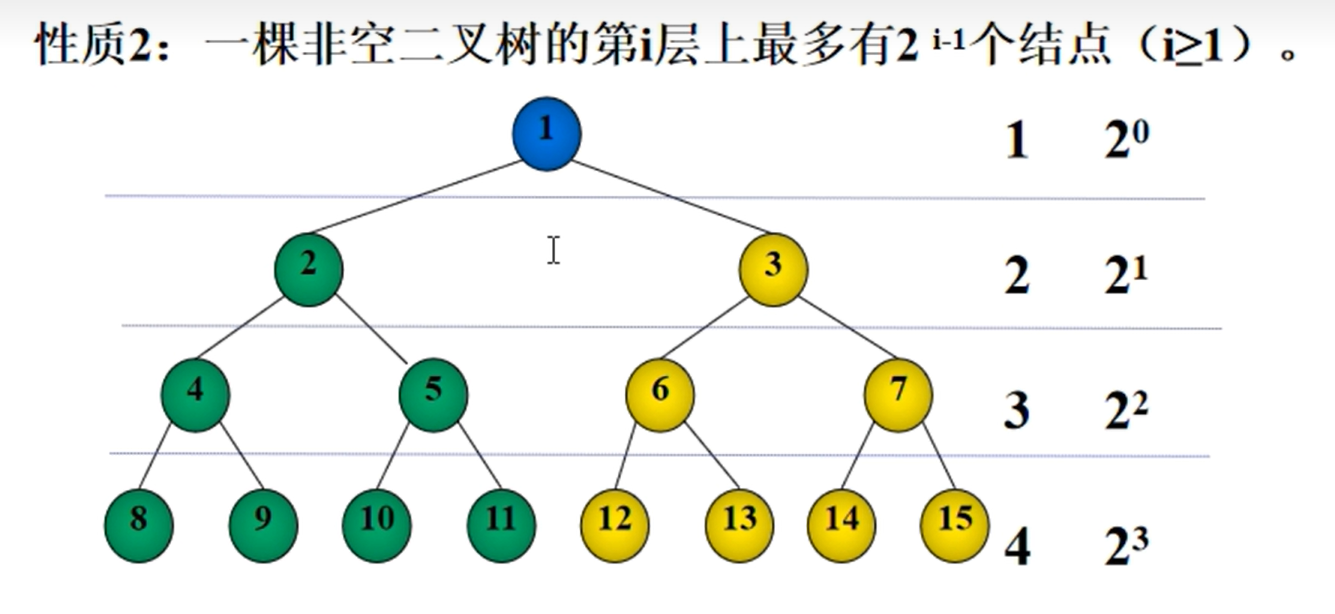
0,度为2的节点数为n2,则有n0=n2+1对于非空二叉树的第i层上最多有2^i-1^个节点(满二叉树)
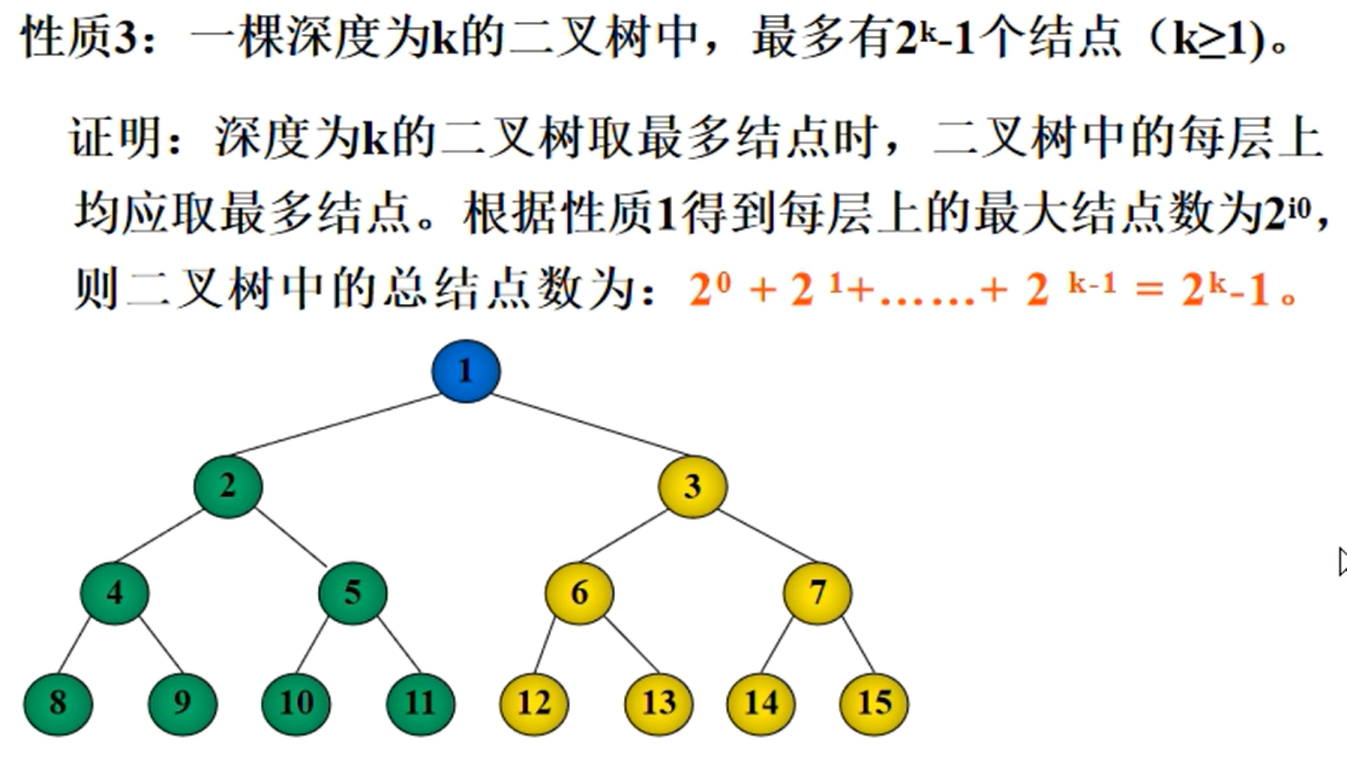
一颗深度为k的二叉树中,最多有2^k^-1个节点(满二叉树)
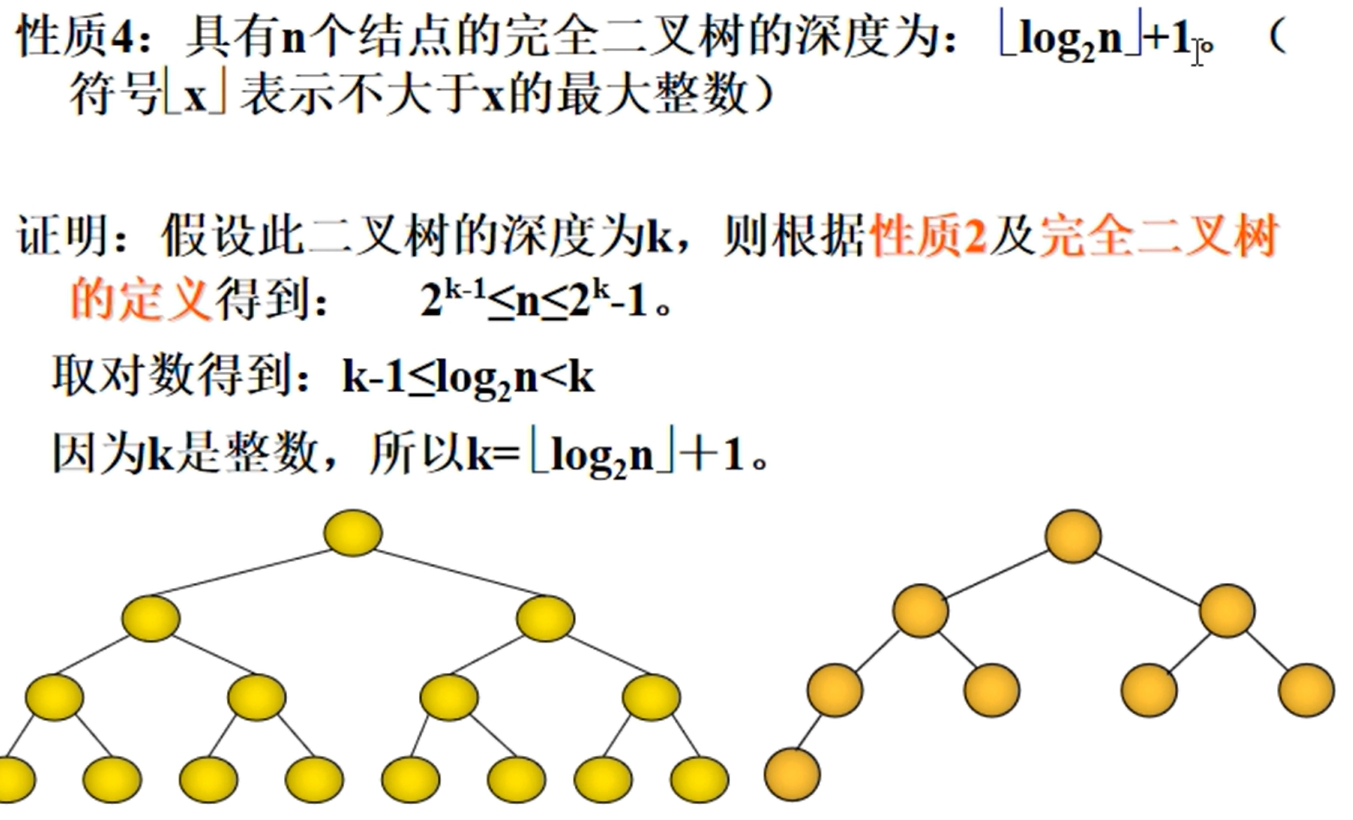
具有n个节点的完全二叉树的深度为:$\lfloor log_2n \rfloor+1$
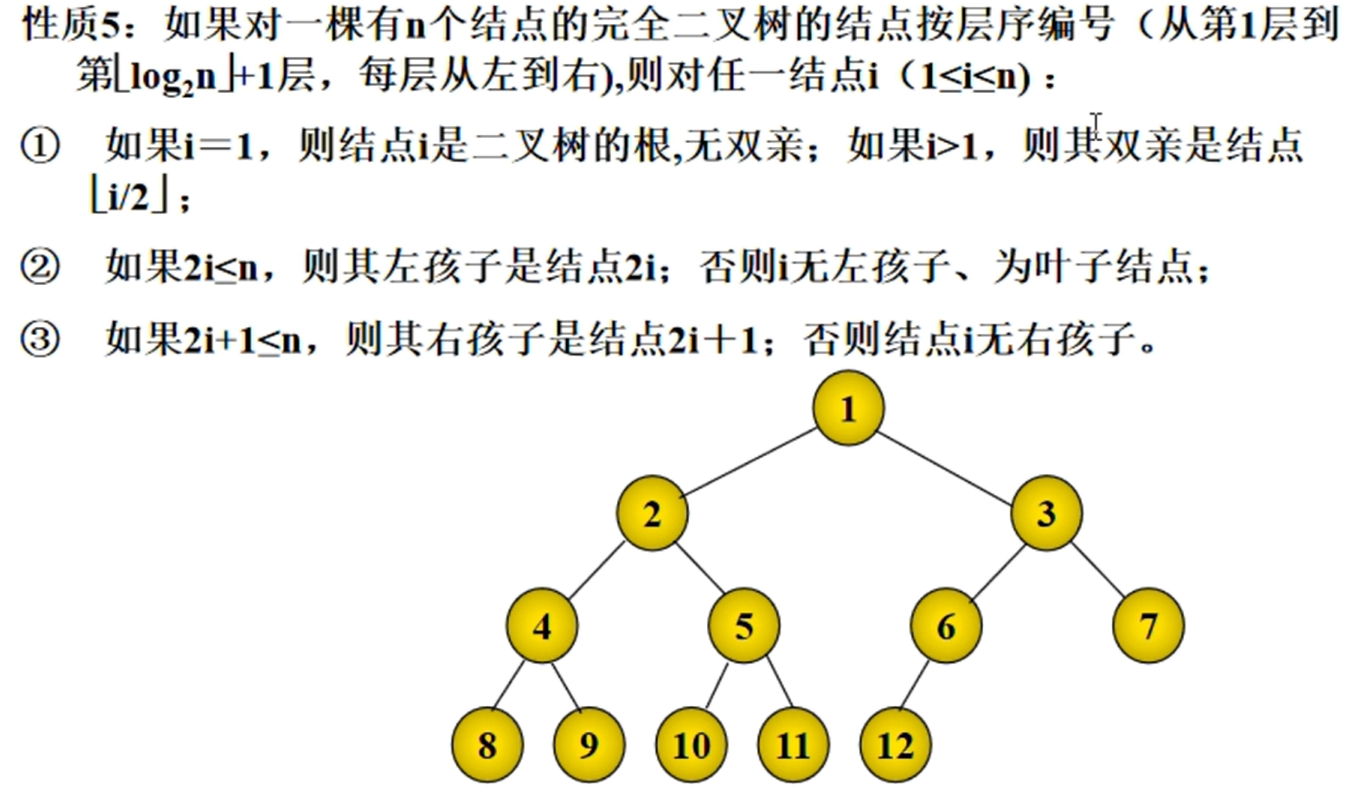
如果对于一颗有n个节点的完全二叉树的节点按层序编号,则对任意节点i(1<=i<=n)
如果i=1,则节点i时二叉树的根节点,如果i>1,则其父亲节点为$\lfloor i/2 \rfloor$
如果$2i\leq n$,则其左孩子是节点2i,否则i无左孩子,为叶子节点
如果$2i+1\leq n$,其右孩子是节点2i+1,否则节点i无右孩子

完全二叉树
满二叉树
存储方式
顺序存储(用列表或者数组储存)(一般适用于完全二叉树)
链式存储
列表存储
二叉树的创建
层次按序创建
1 | class TreeNode: |
函数前序创建
1 | def creat_binary_tree(input_list=[]): |
二叉树的遍历
- 递归遍历
- 非递归遍历
- 前序遍历
- 中序遍历
- 后序遍历
- 层次遍历
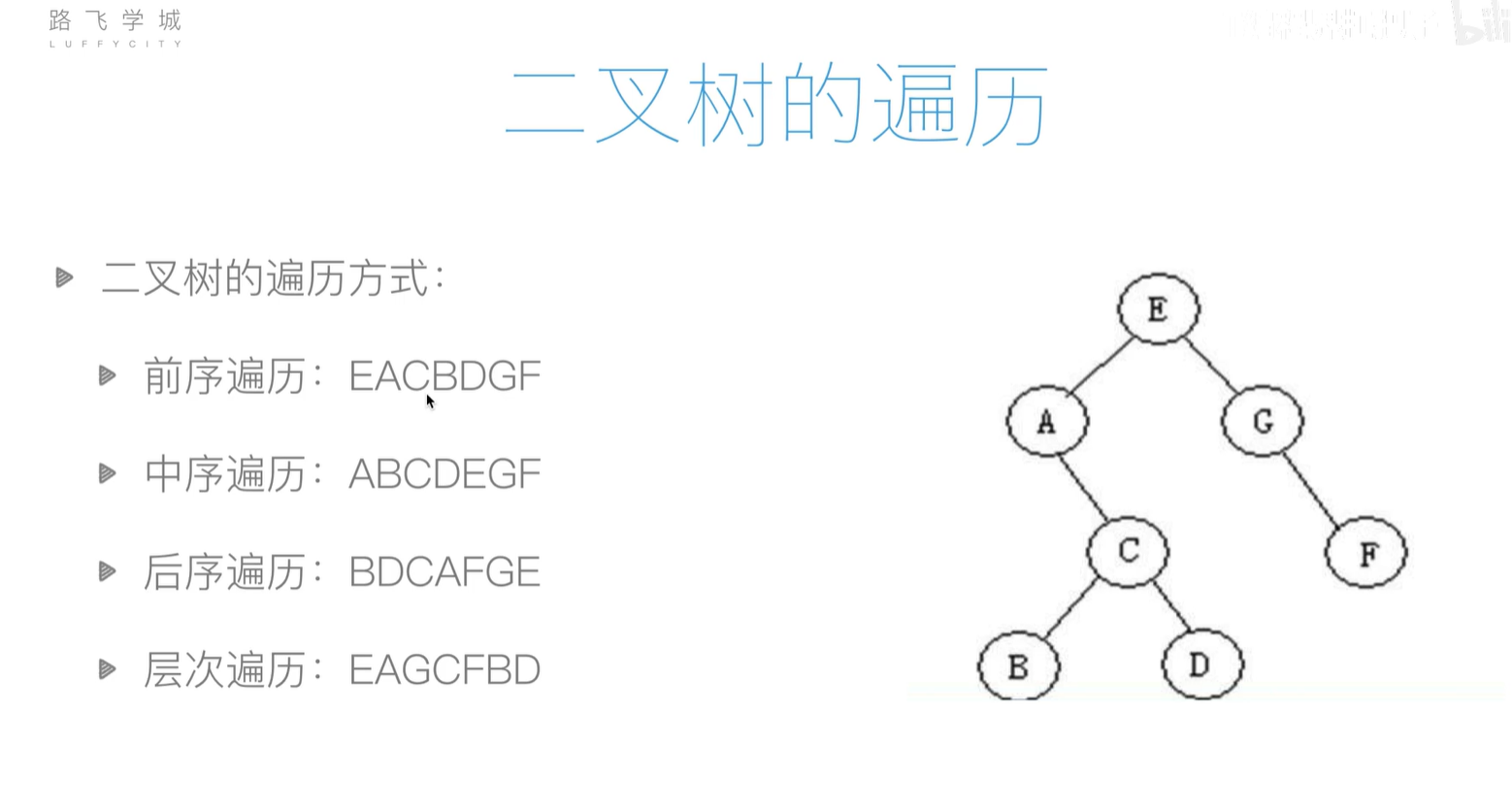
递归遍历代码
1 | def pre_order_traversal(node): |
非递归遍历代码
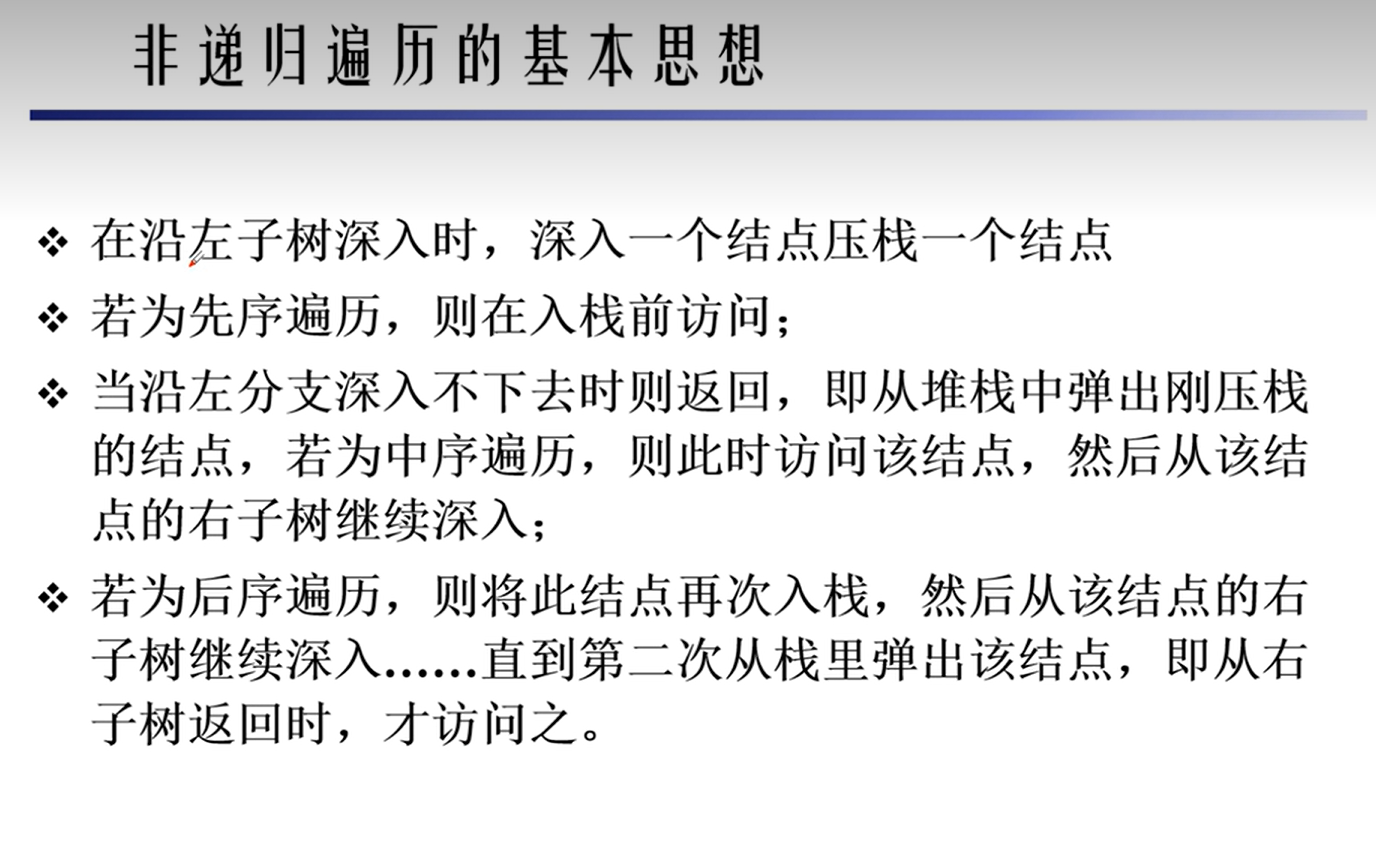
1 | def preorderTraversal(root: TreeNode) -> List[int]: |
哈夫曼树
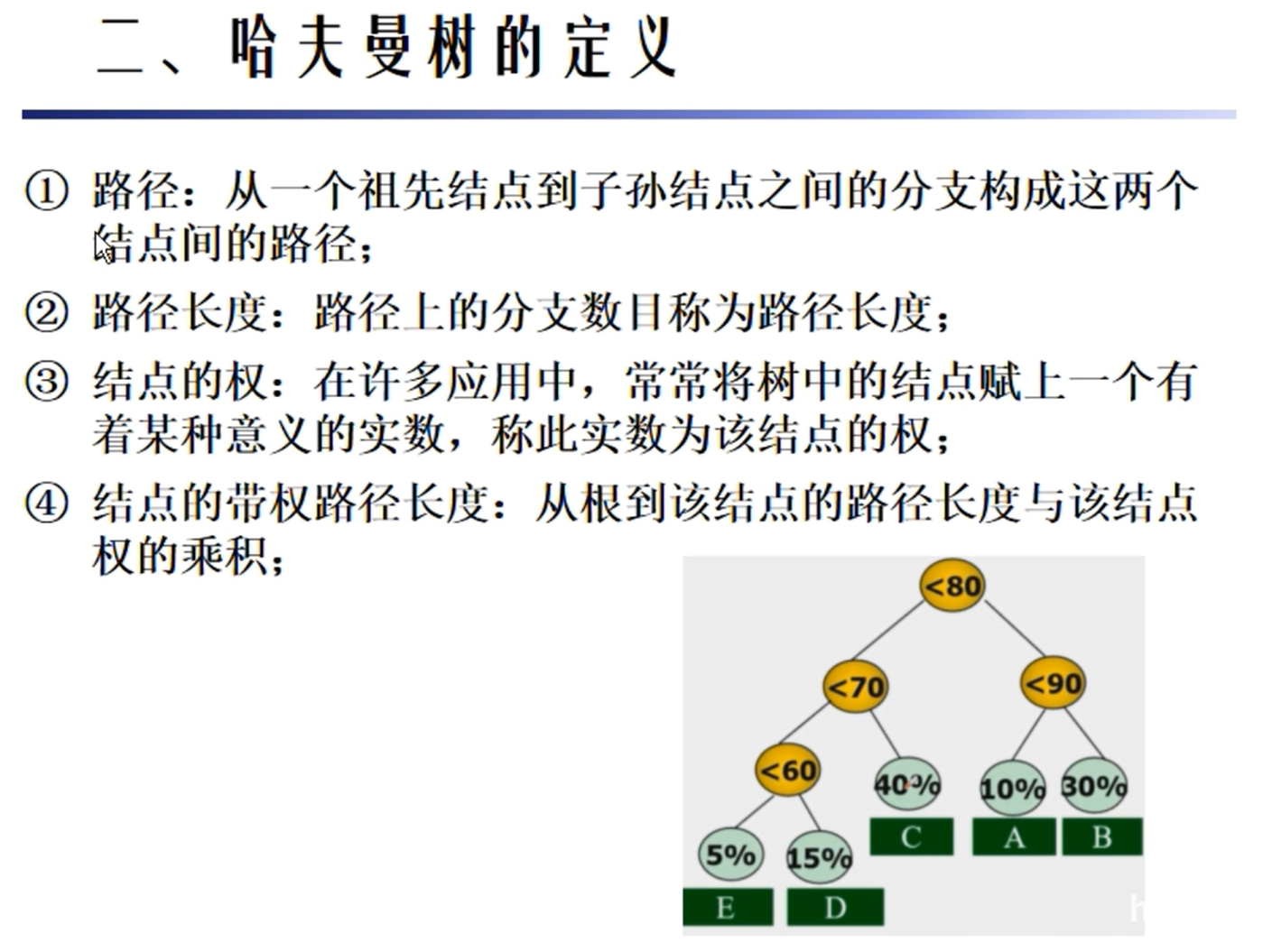
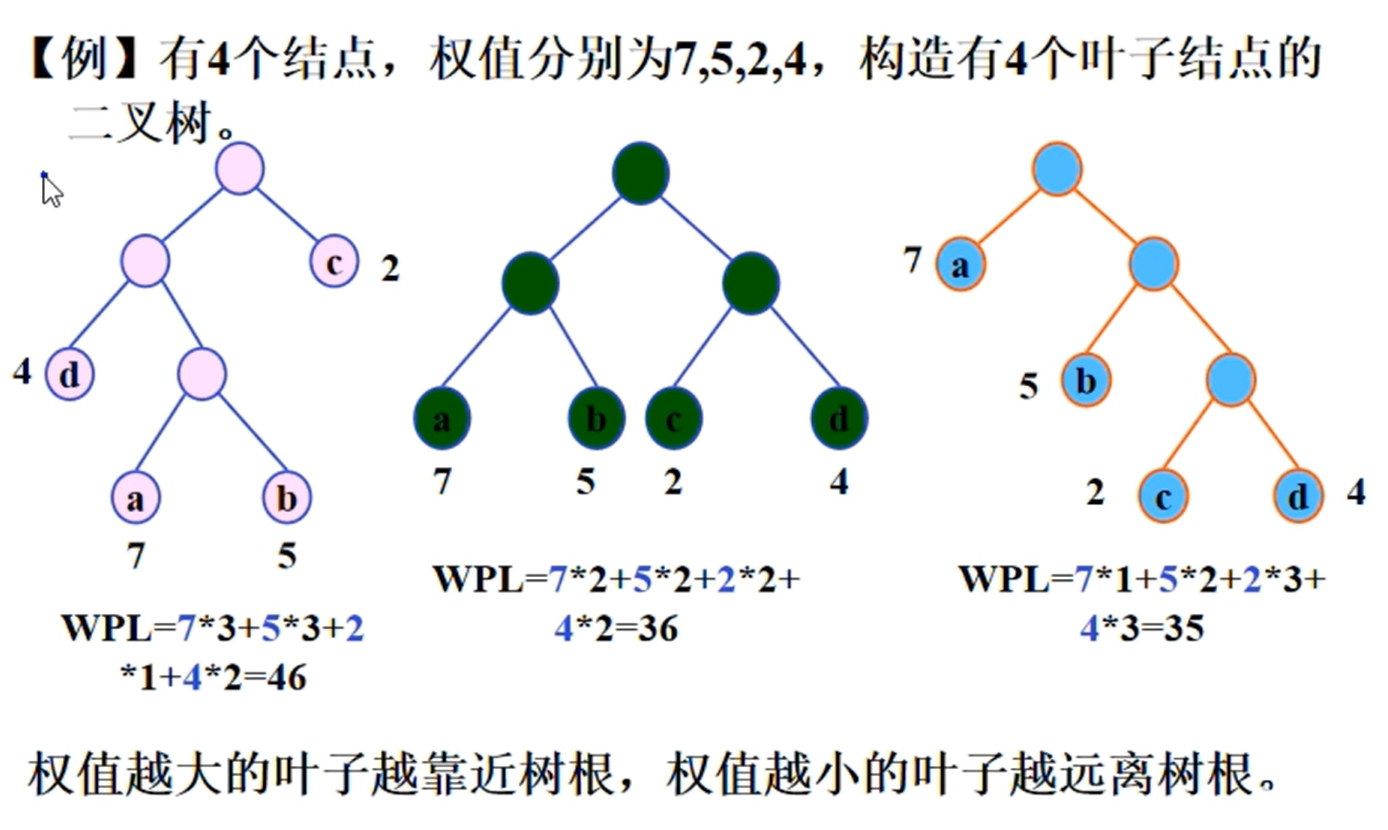

哈夫曼编码
代码
1 | class HuffmanNode: |
二叉搜索树
基本操作
- 插入
- 查询
- 删除
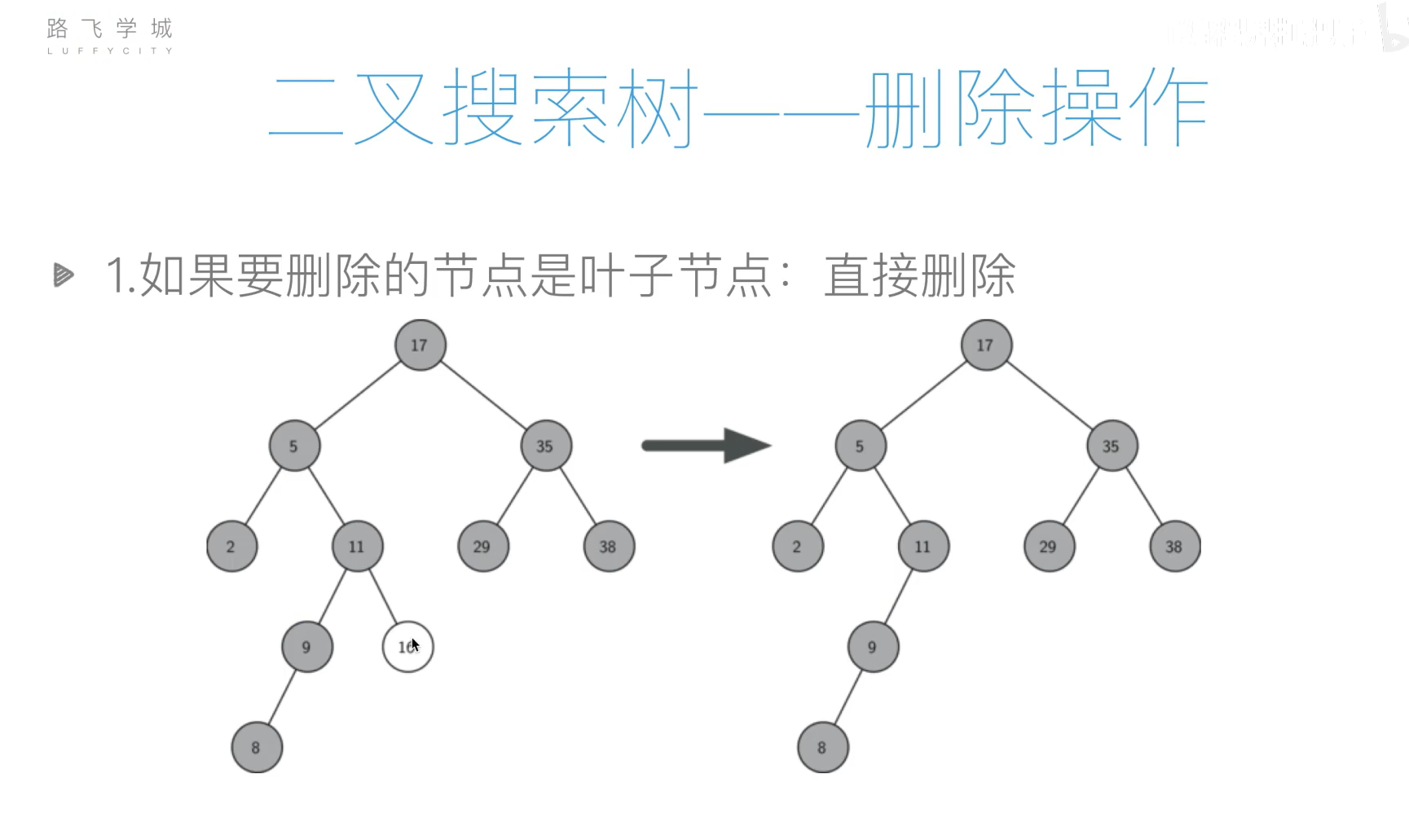
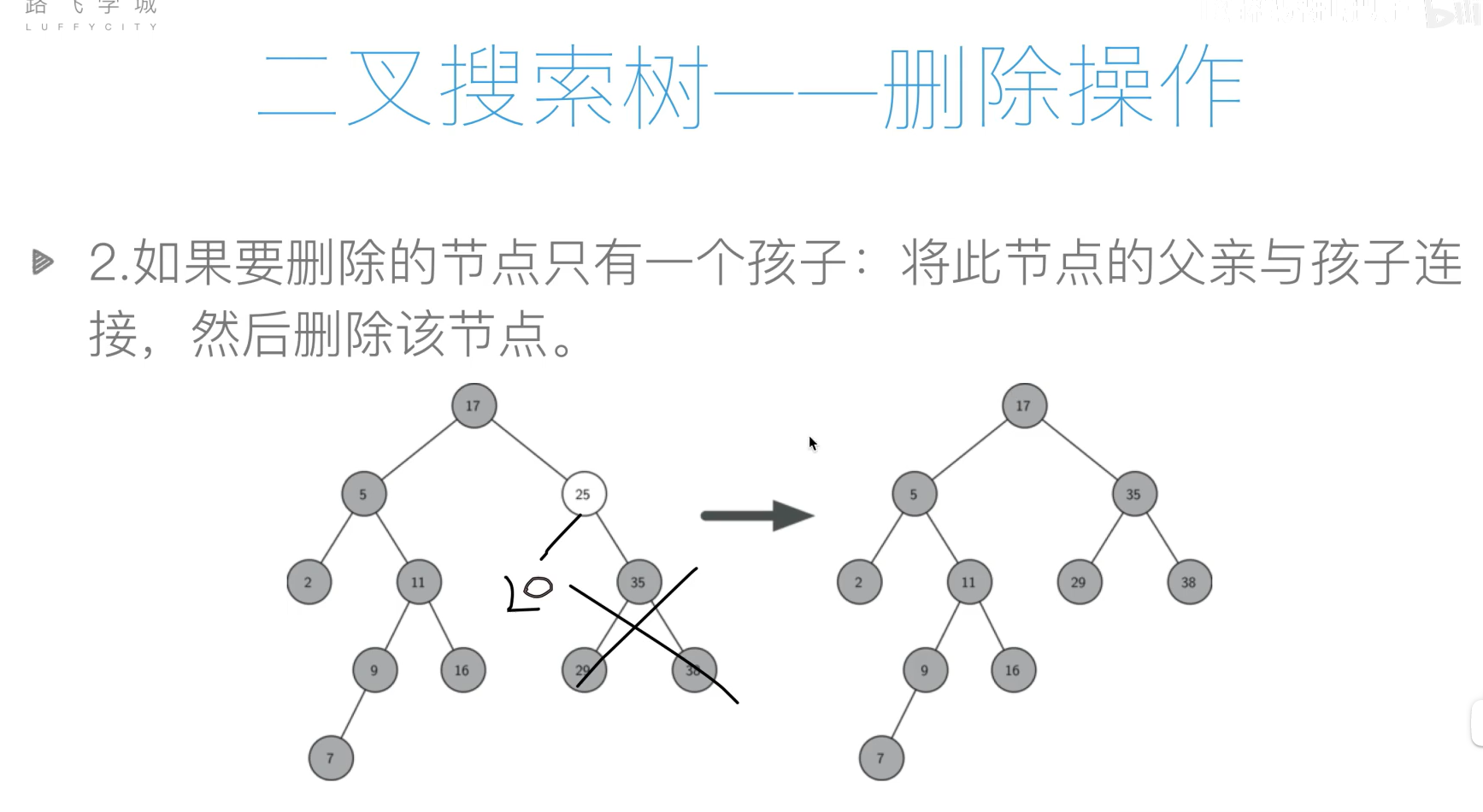
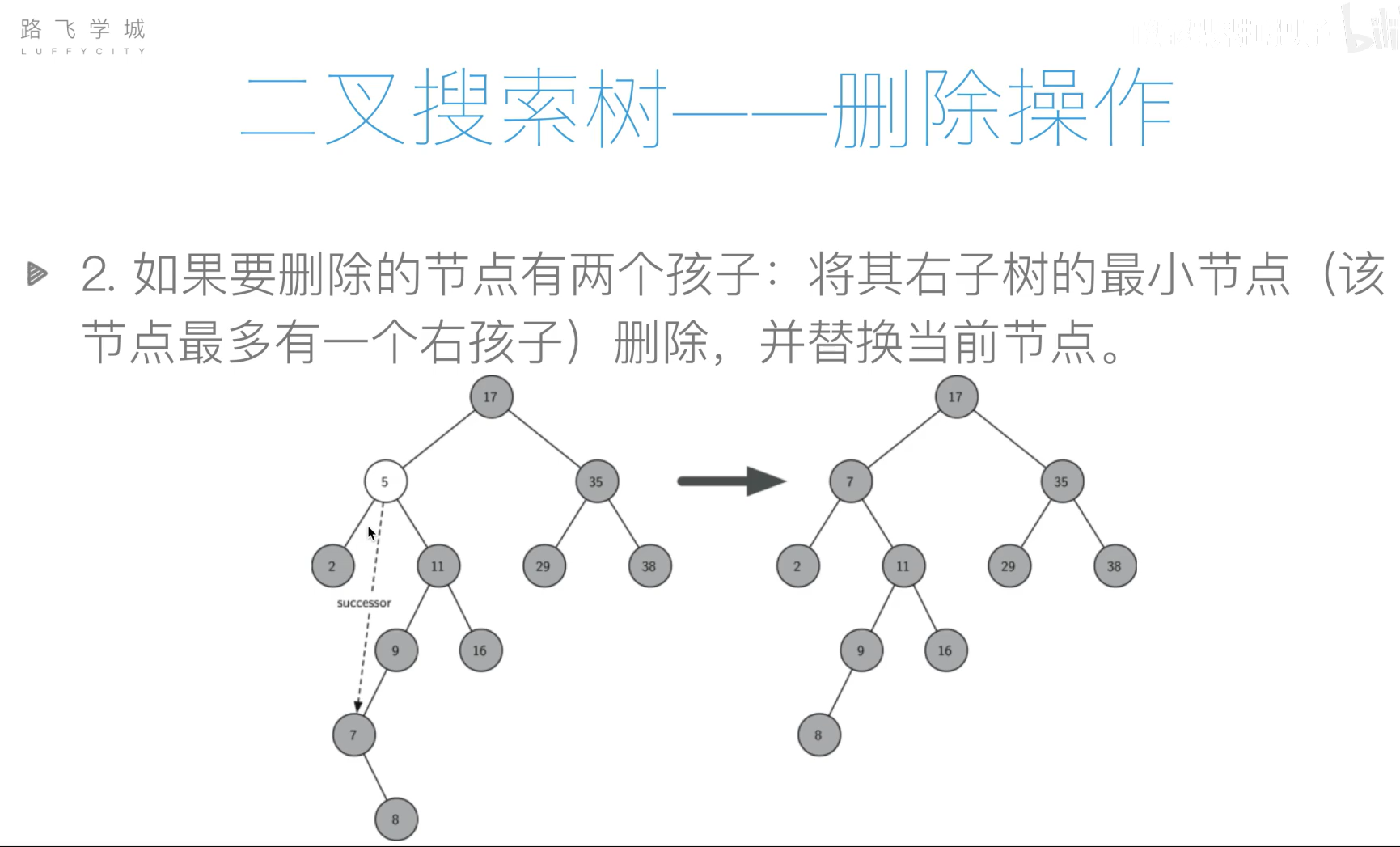
代码
1 | class BiTreeNode: |
AVL树(平衡二叉搜索树)

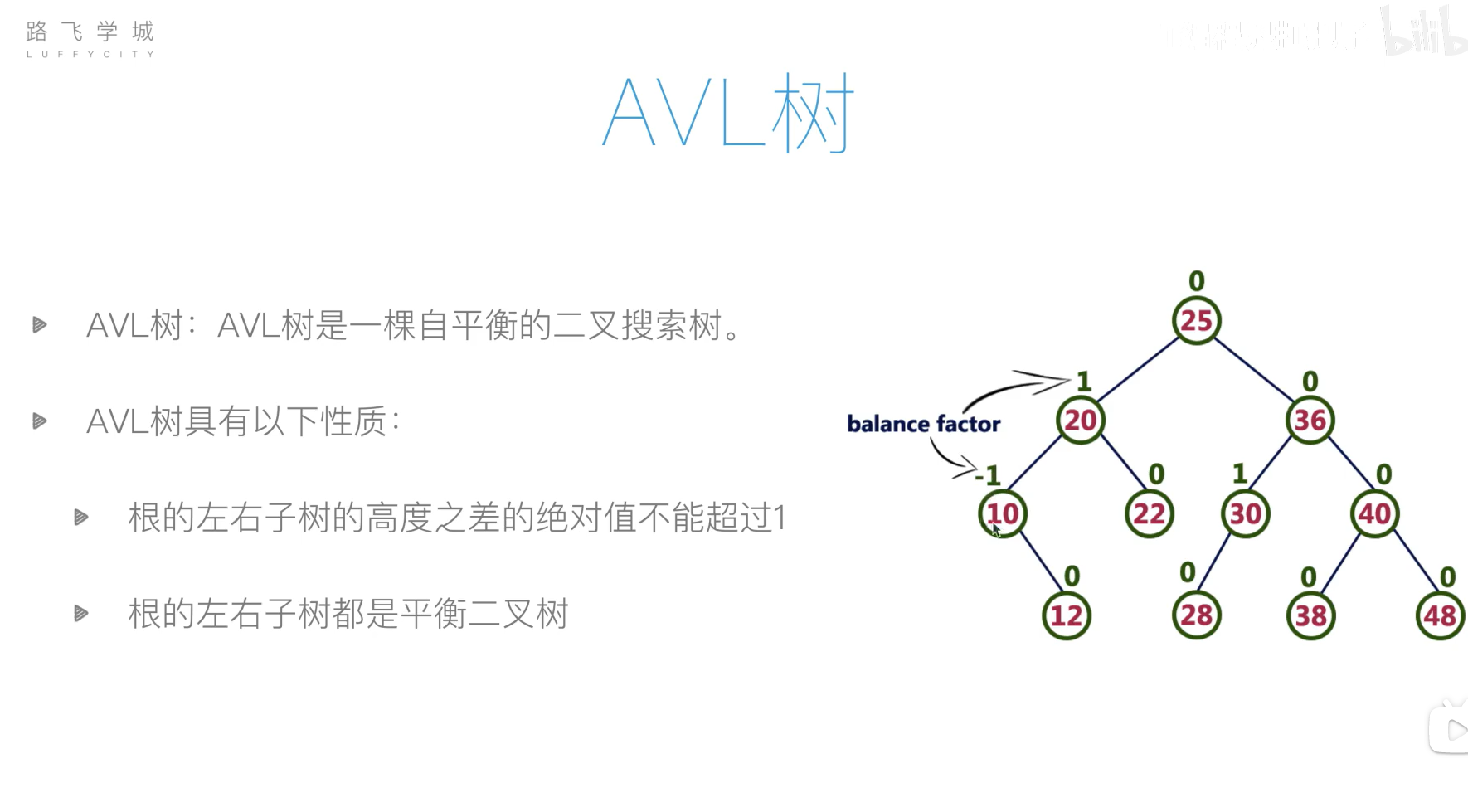

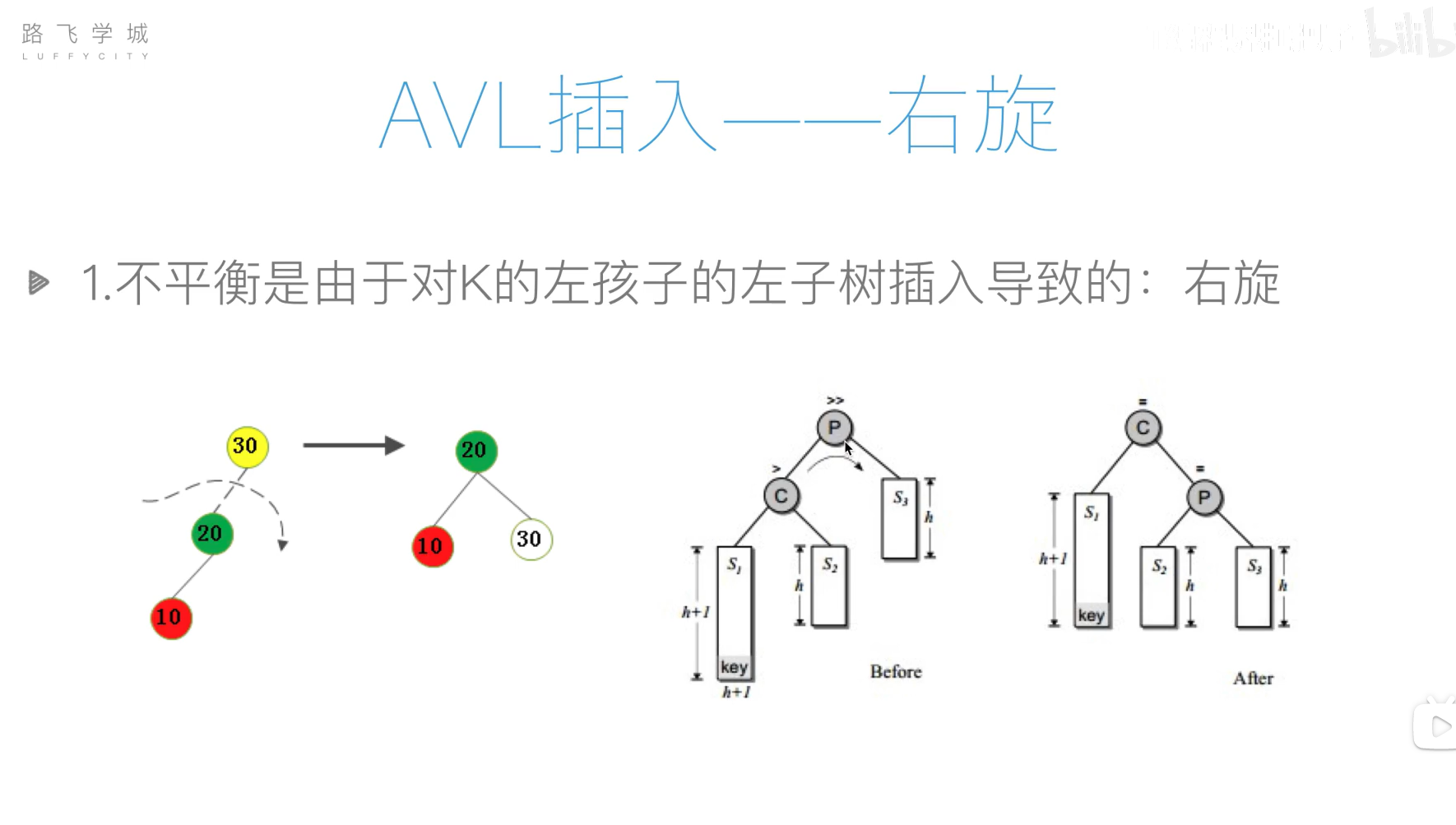
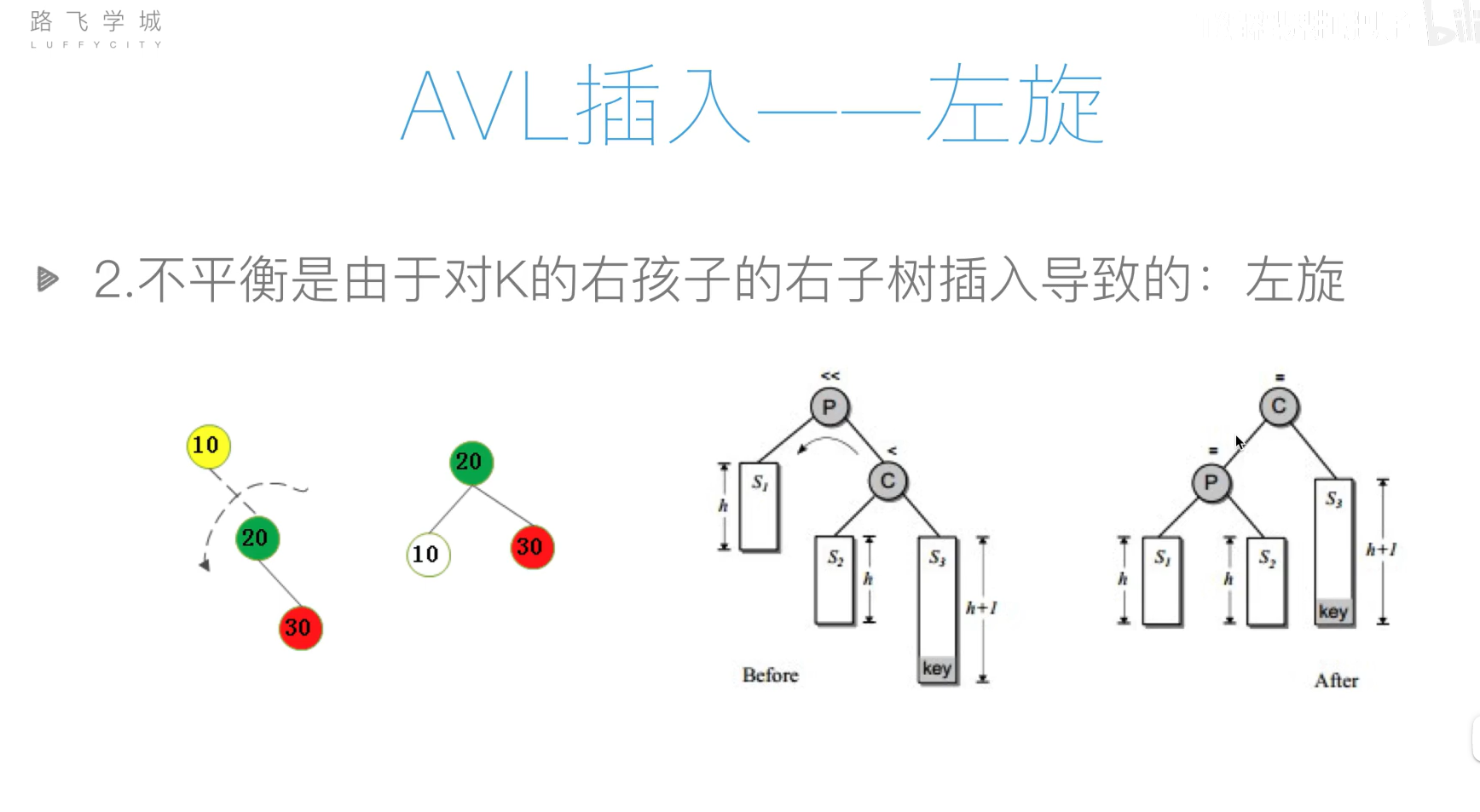
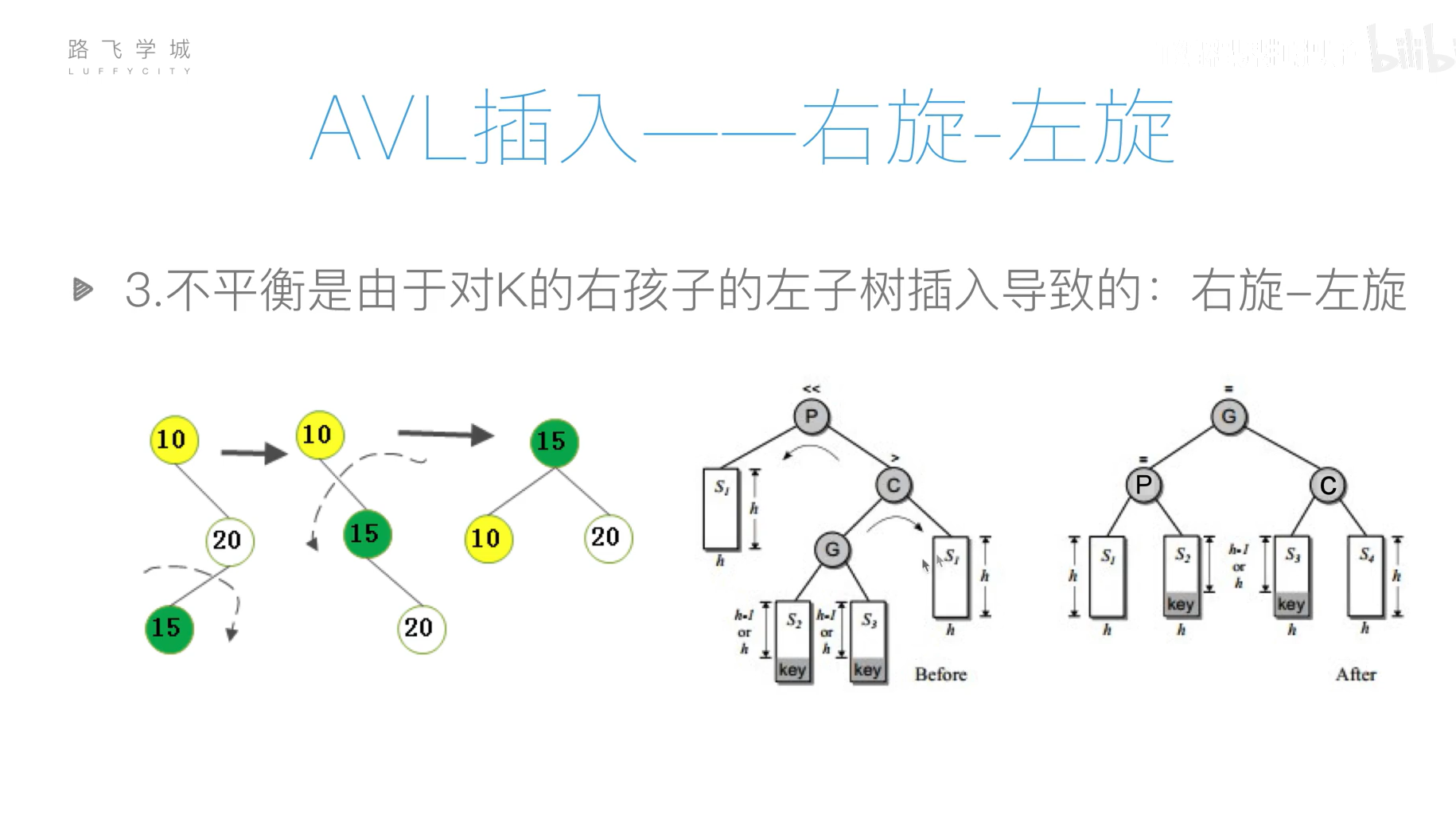

旋转操作过于复杂,可以先将列表元素排好序,然后使用二分递归的方法
代码如下:
二分递归代码
1 | def sortedArrayToBST(nums: list[int]) -> TreeNode: |
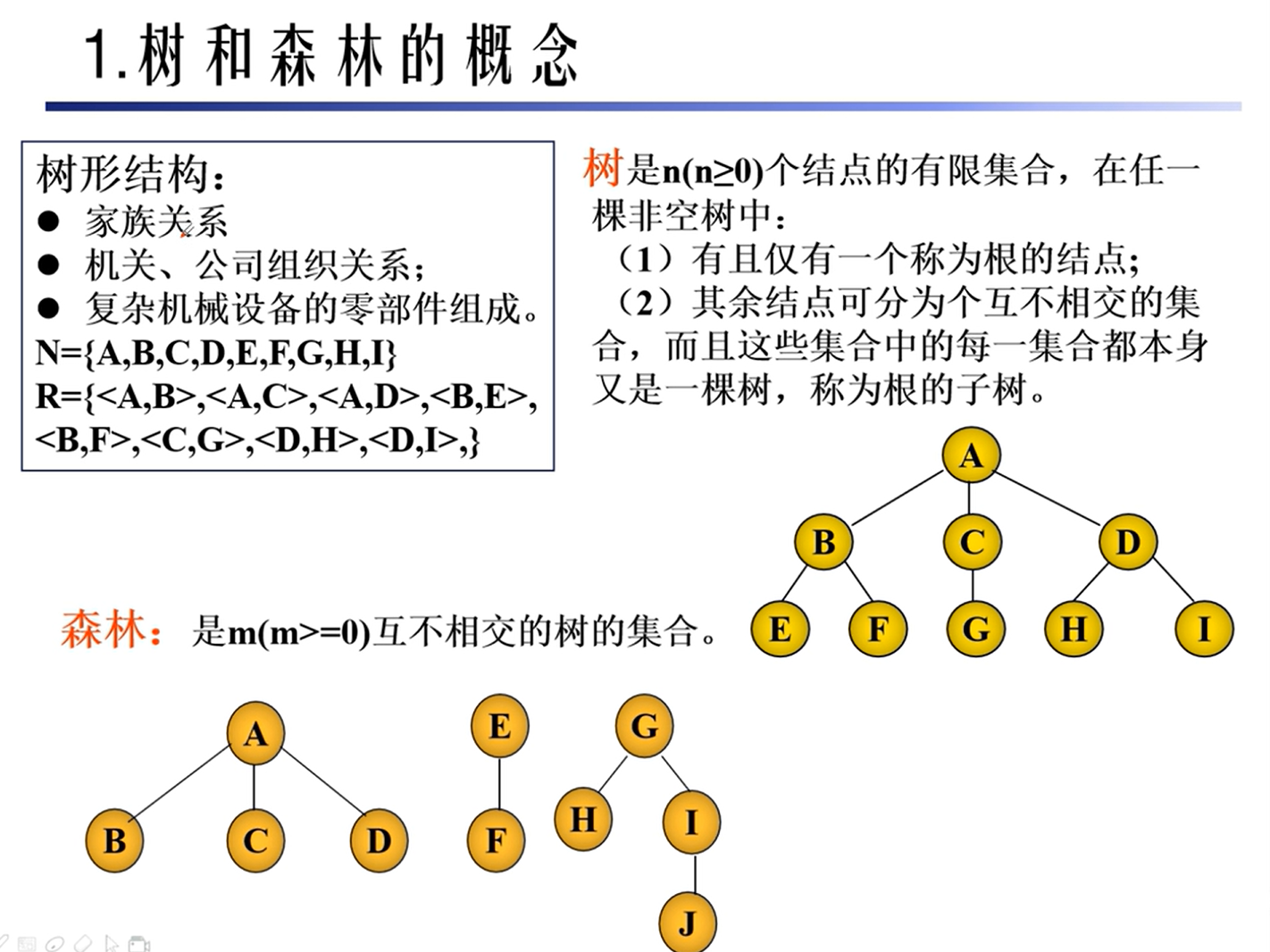
树和森林
基本概念
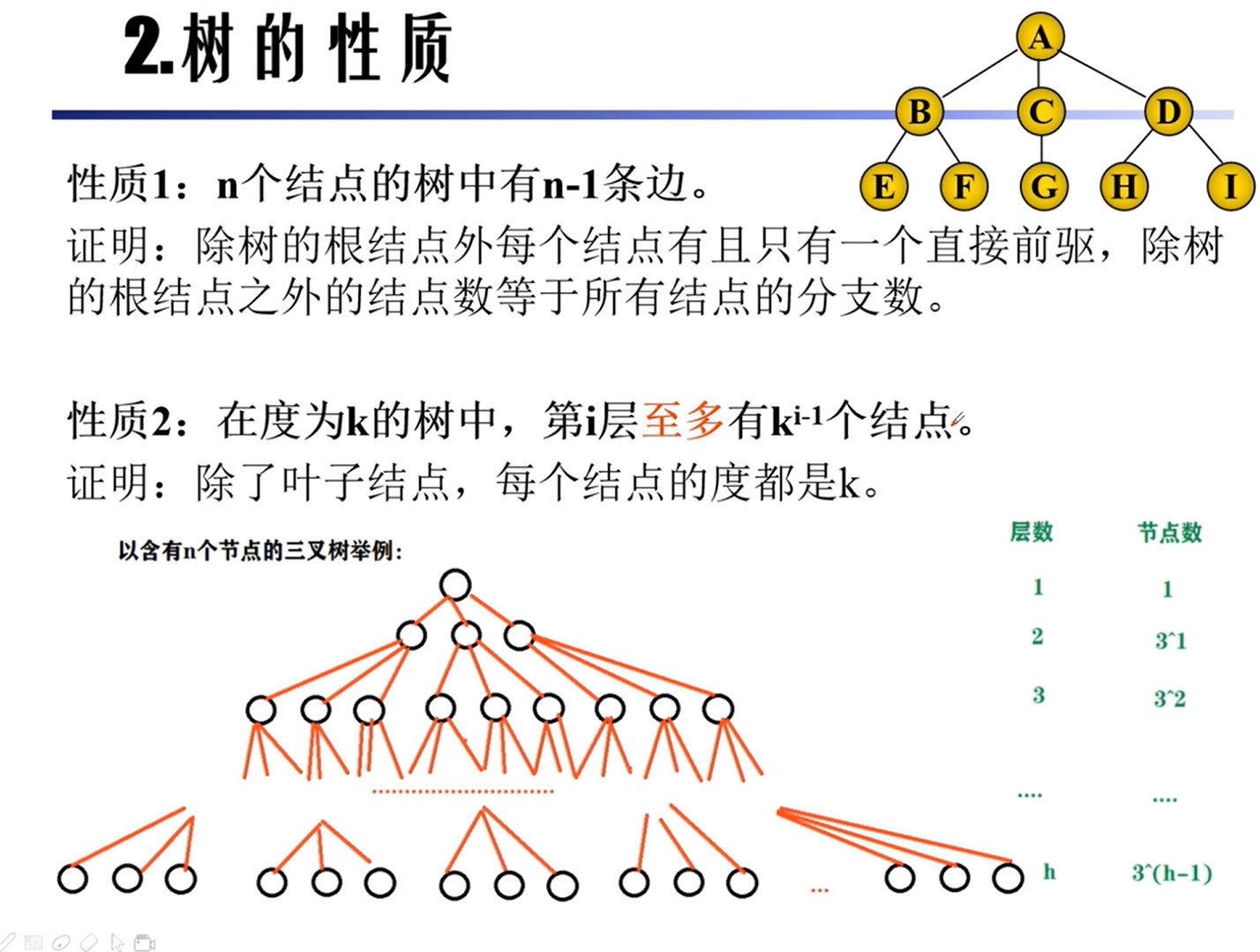
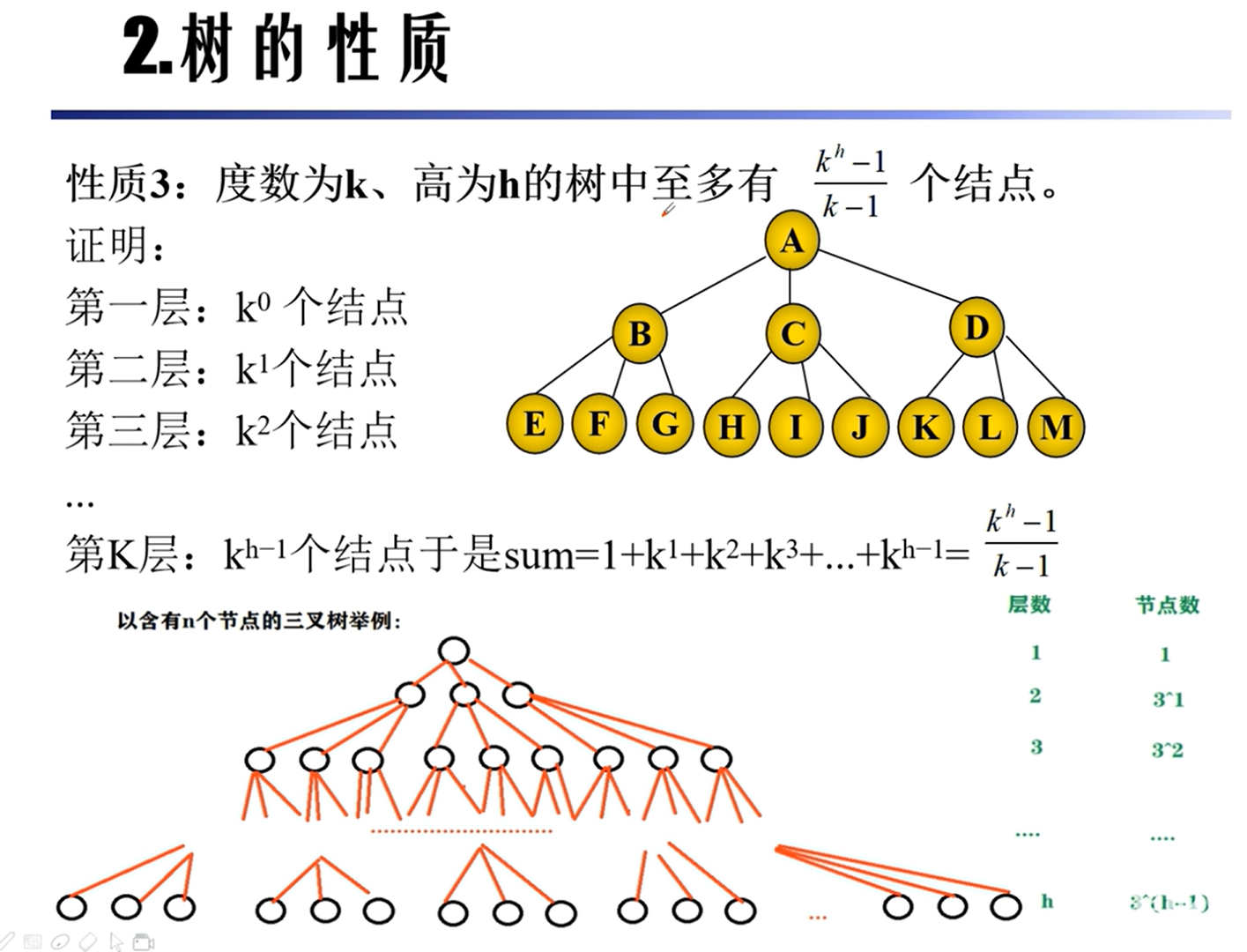
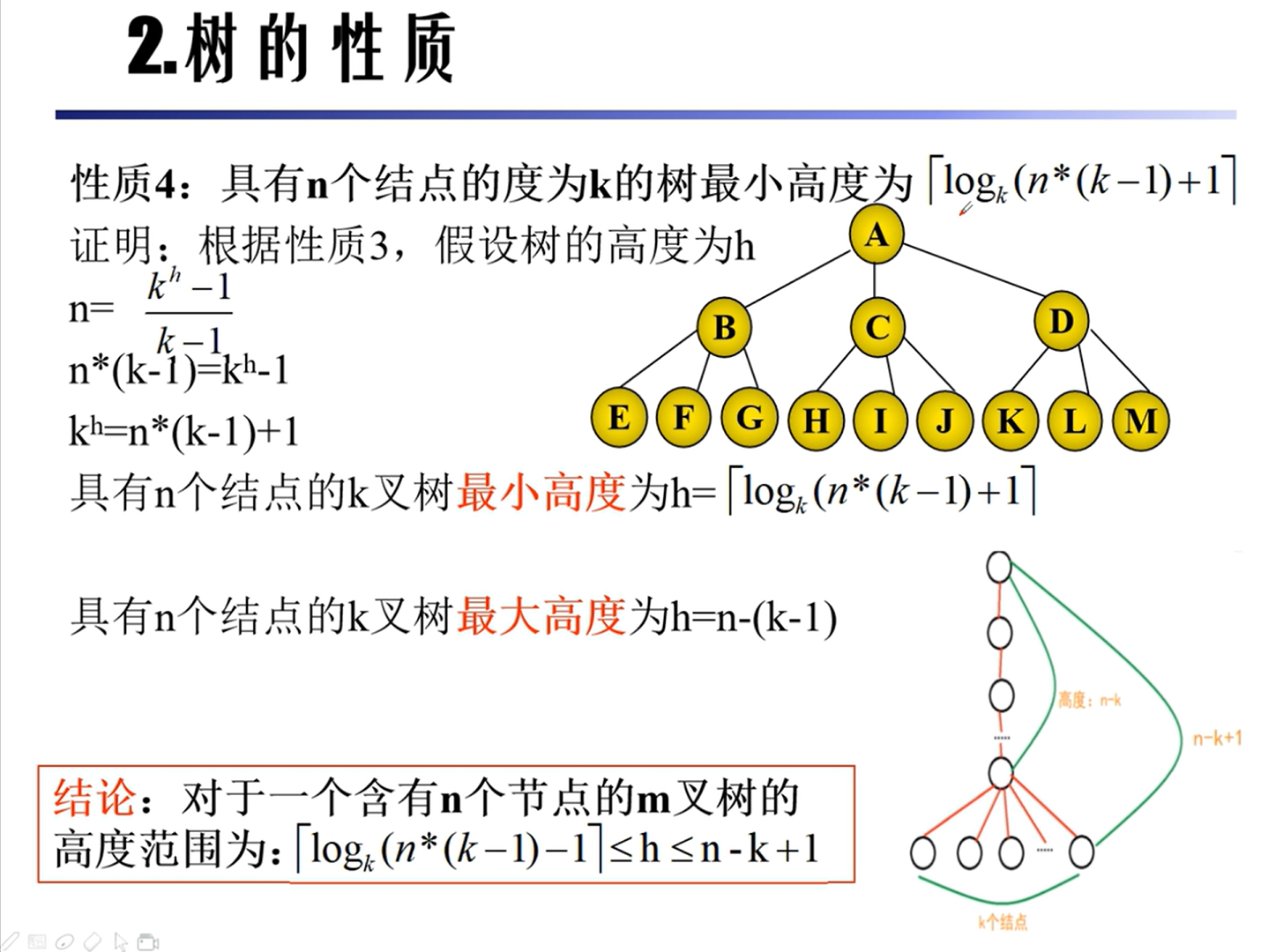
性质
存储

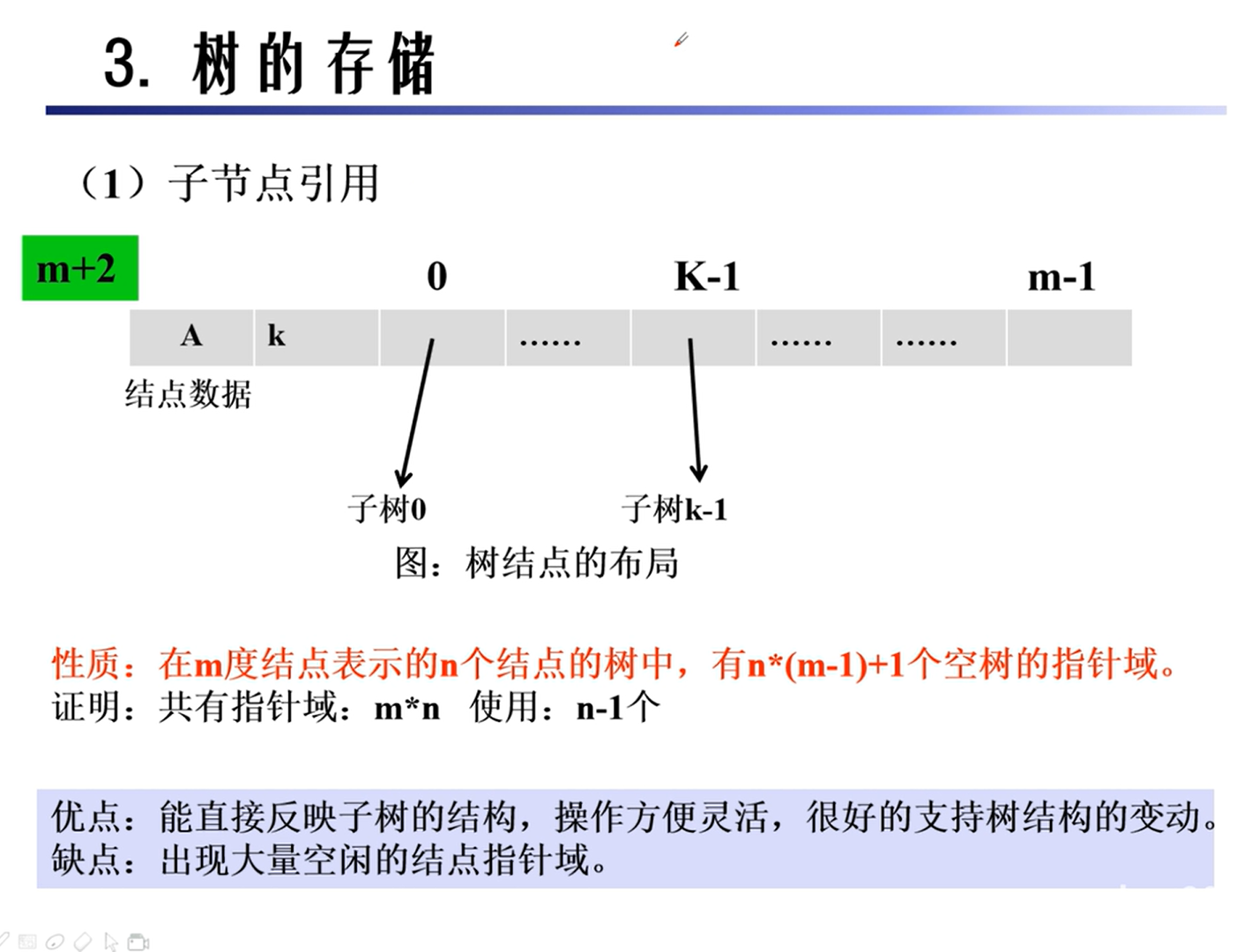
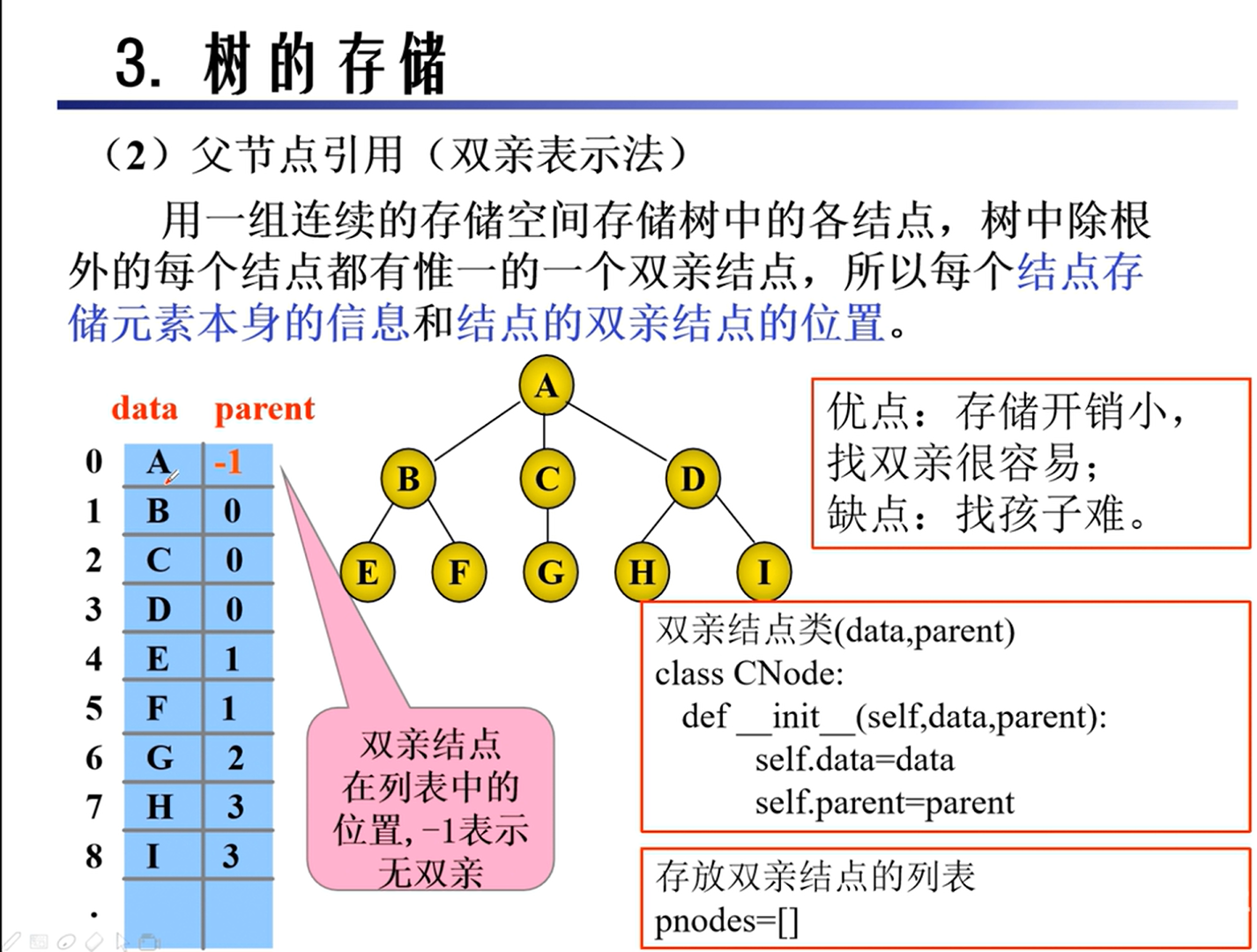
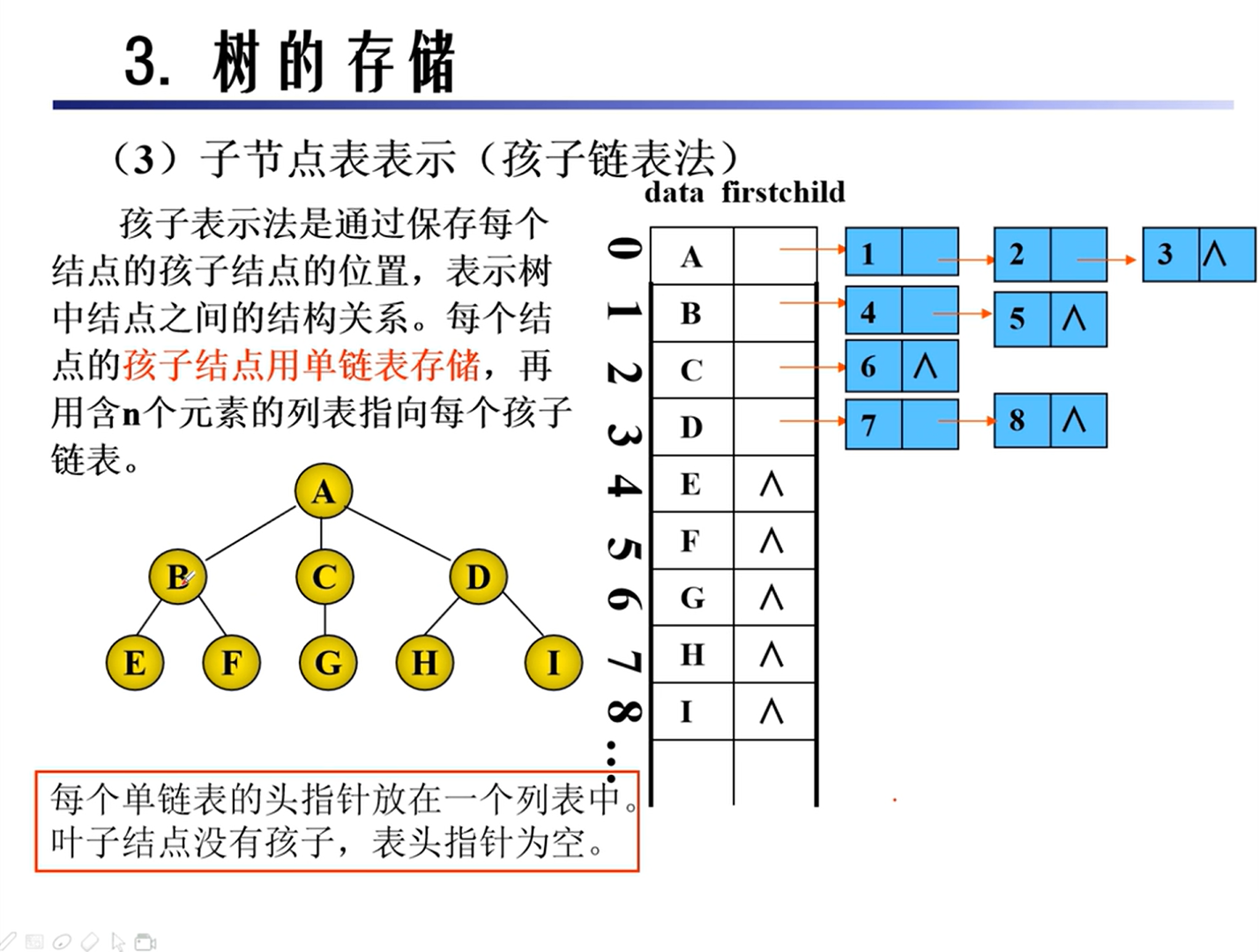
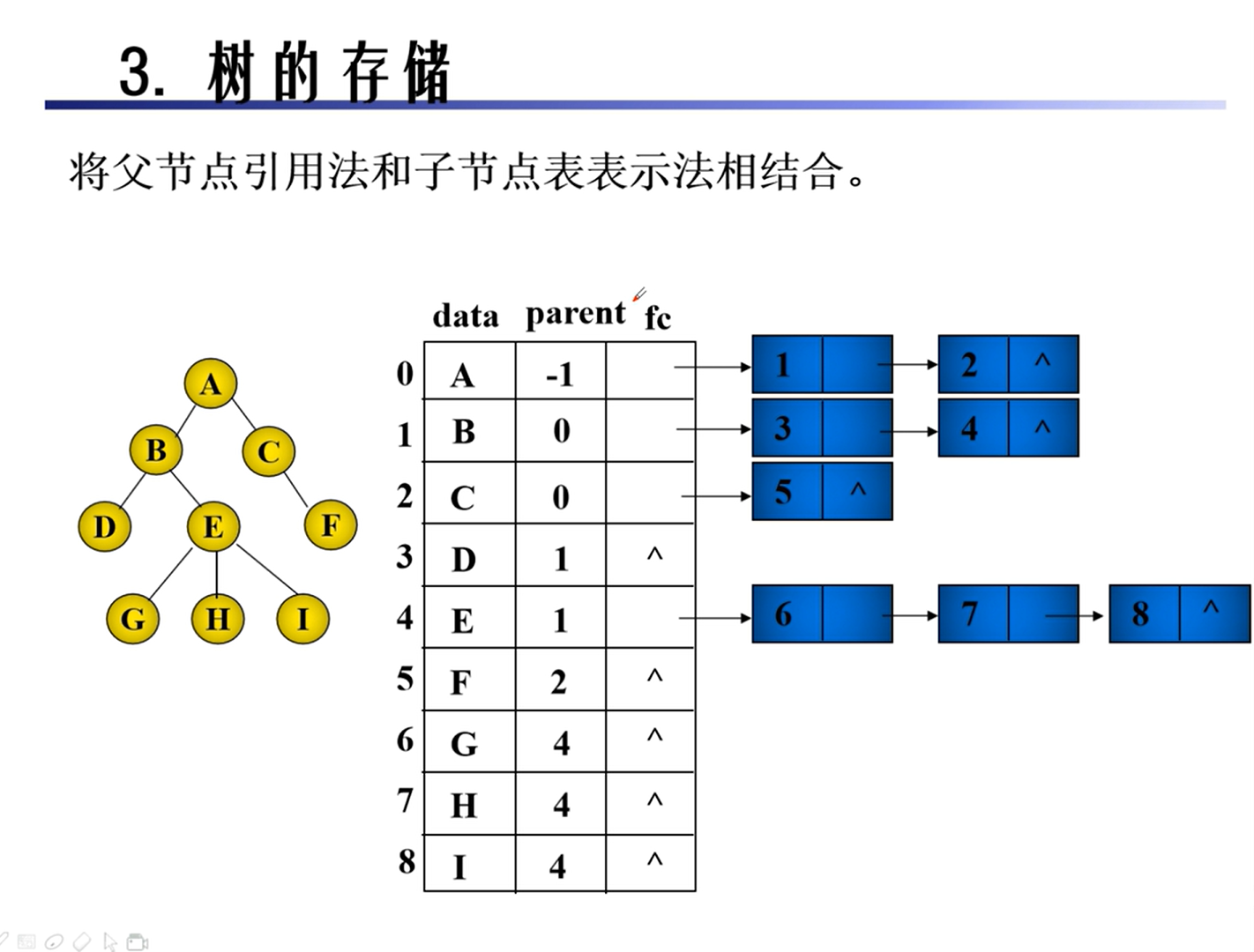
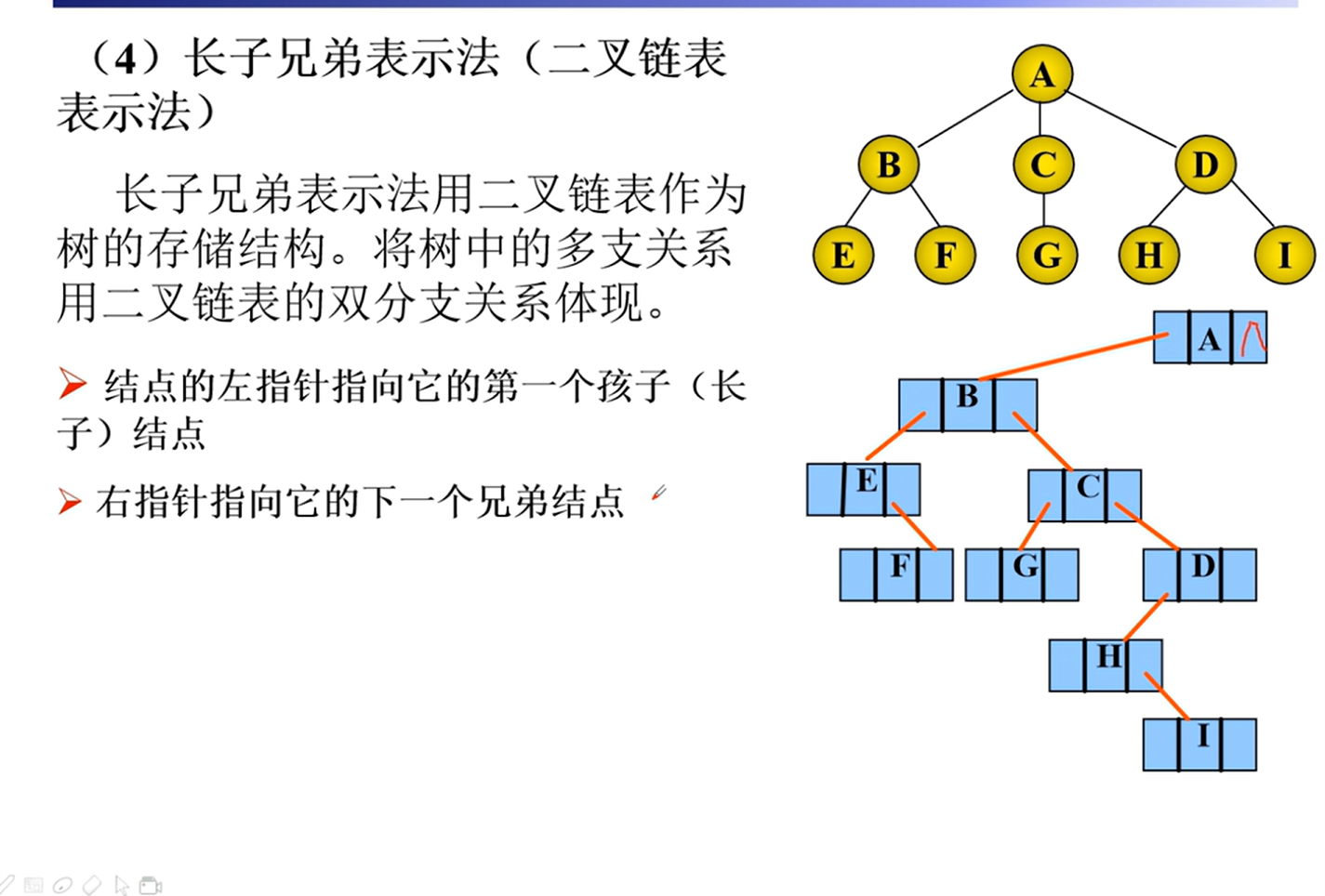
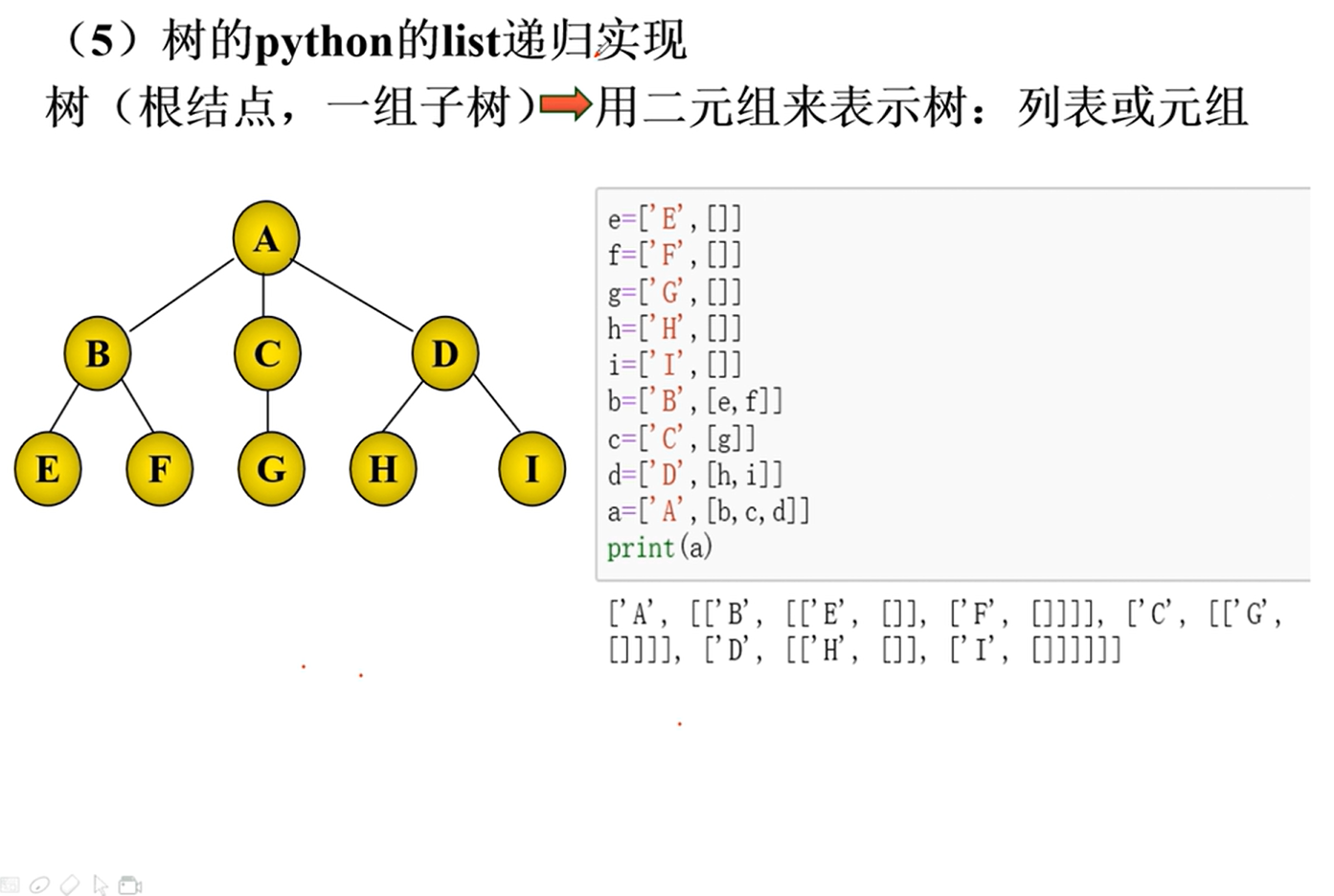
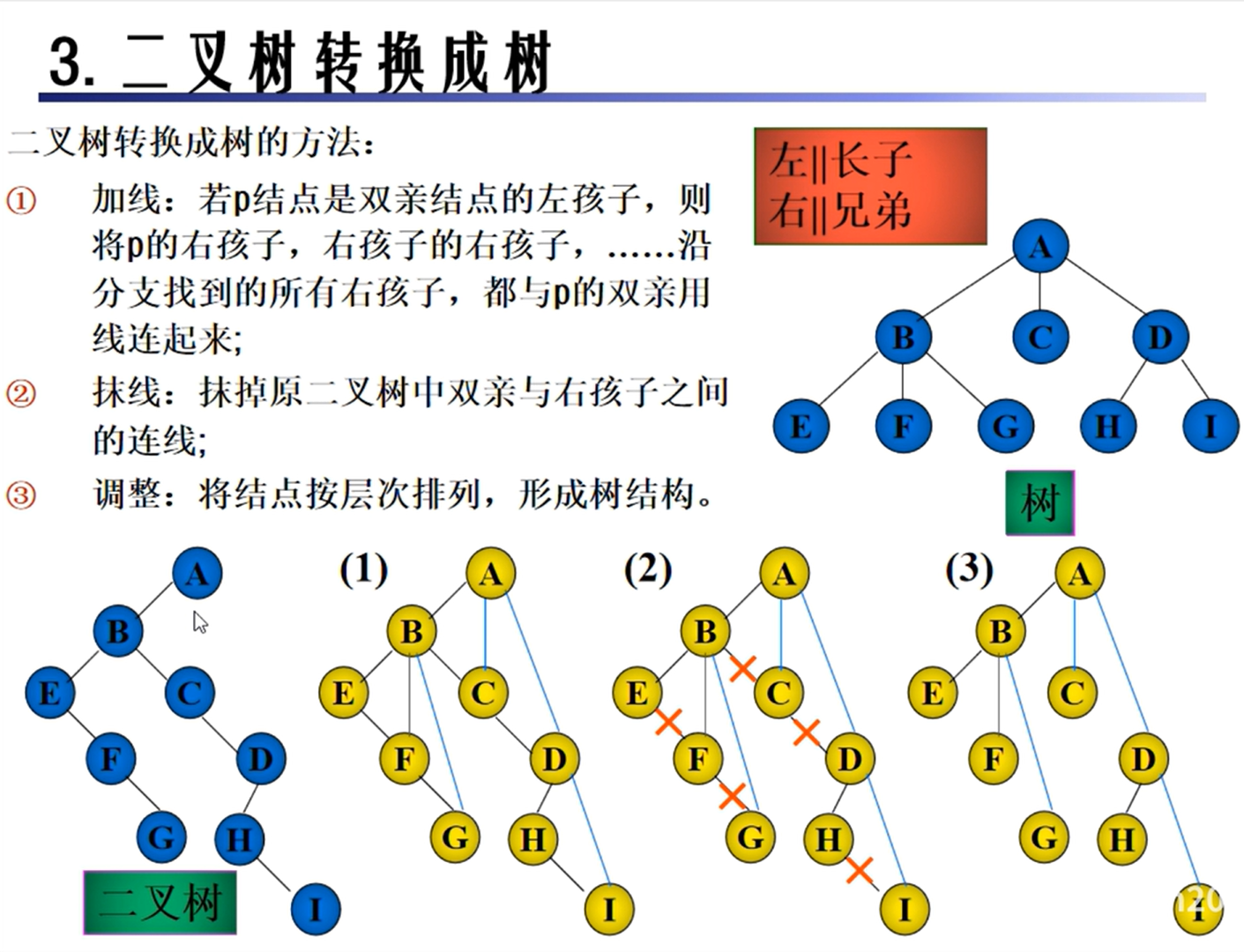
二叉树的转换

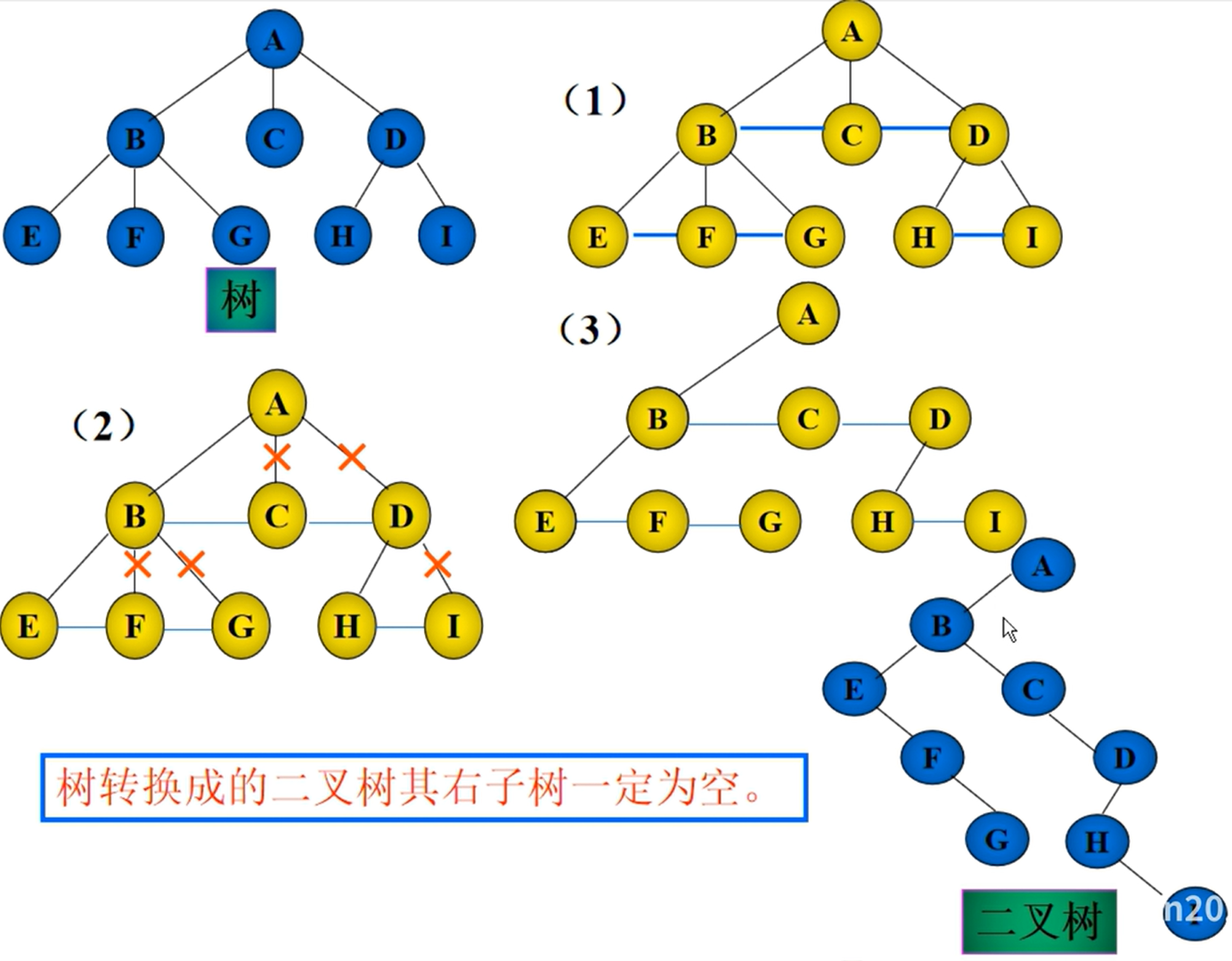

树和森林的转换
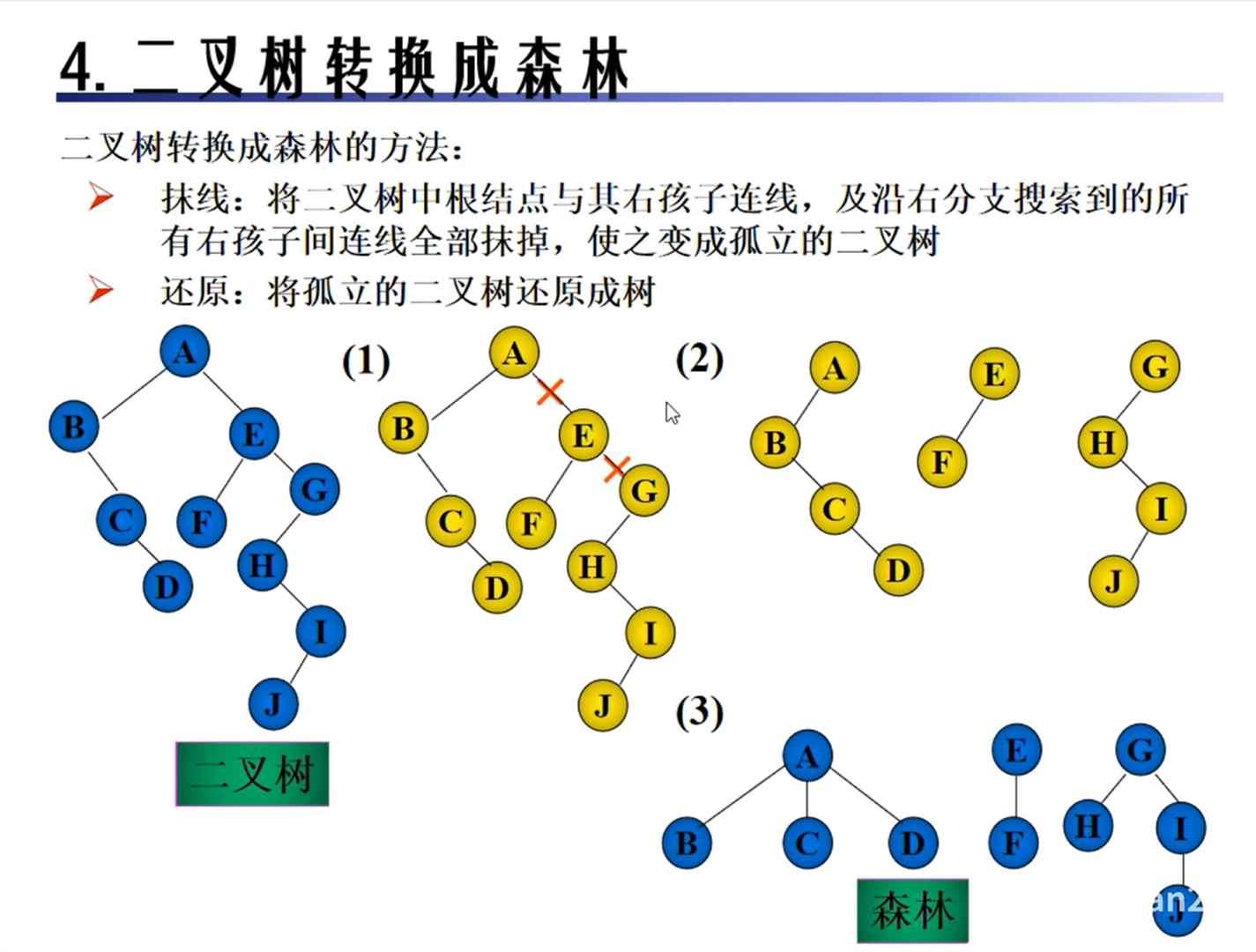
树的遍历
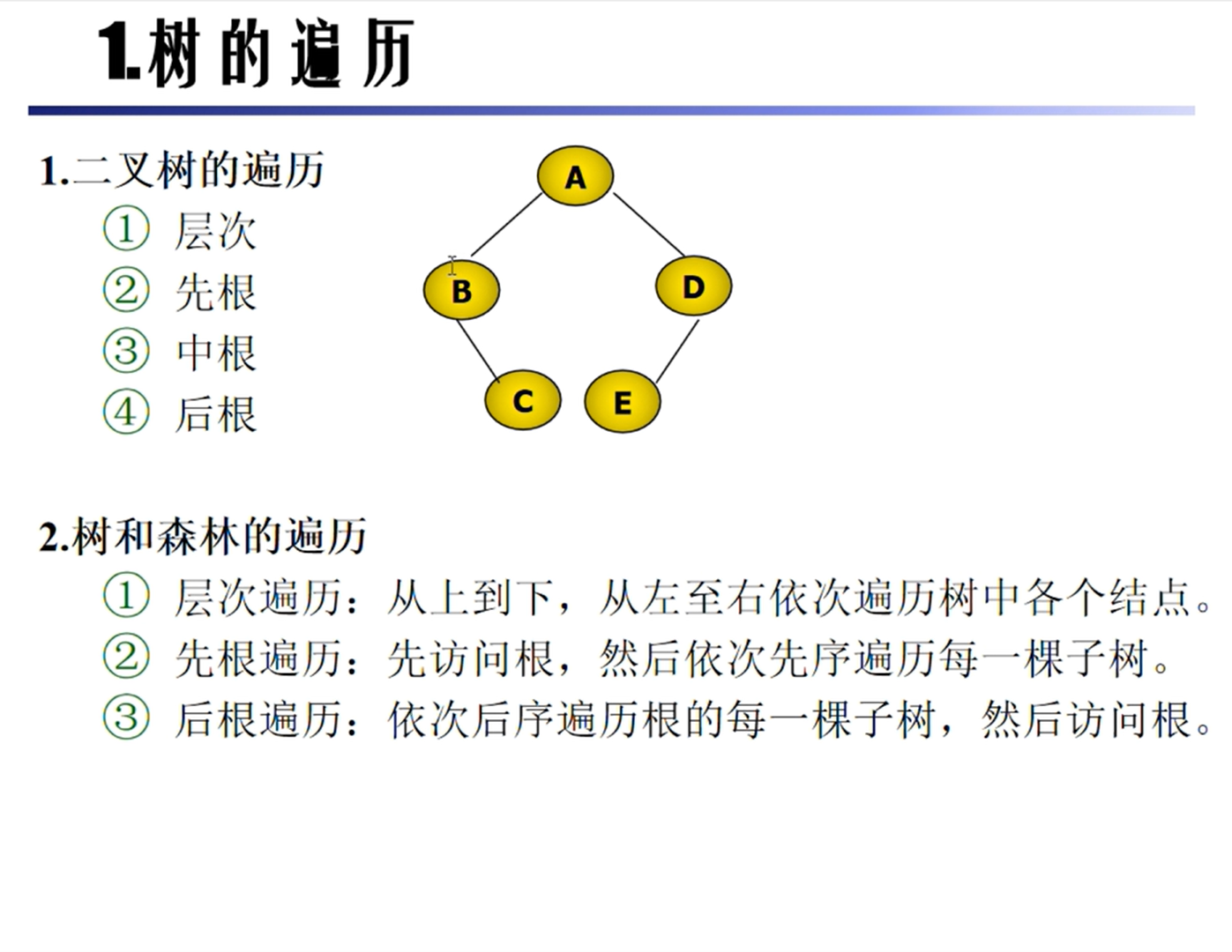
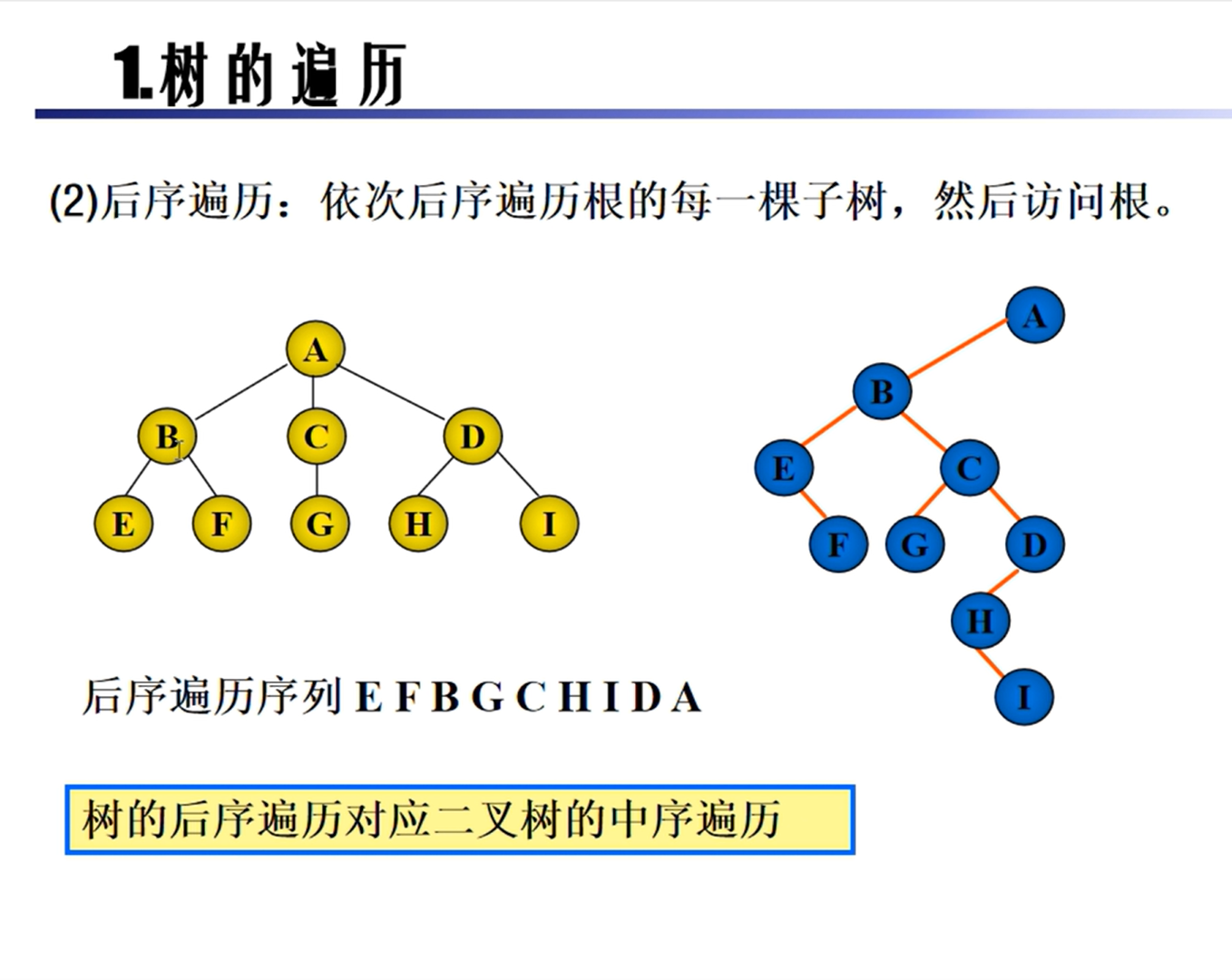
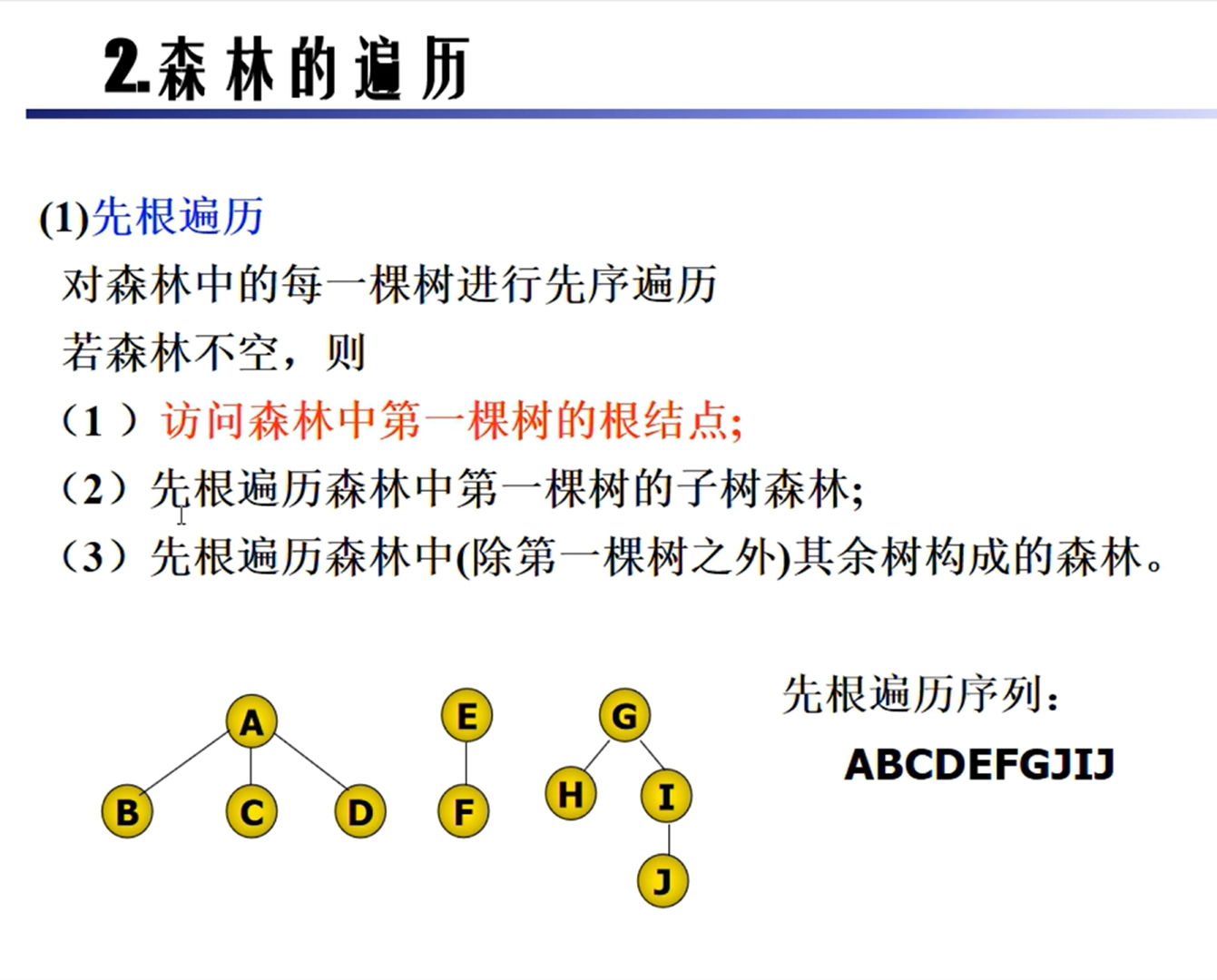
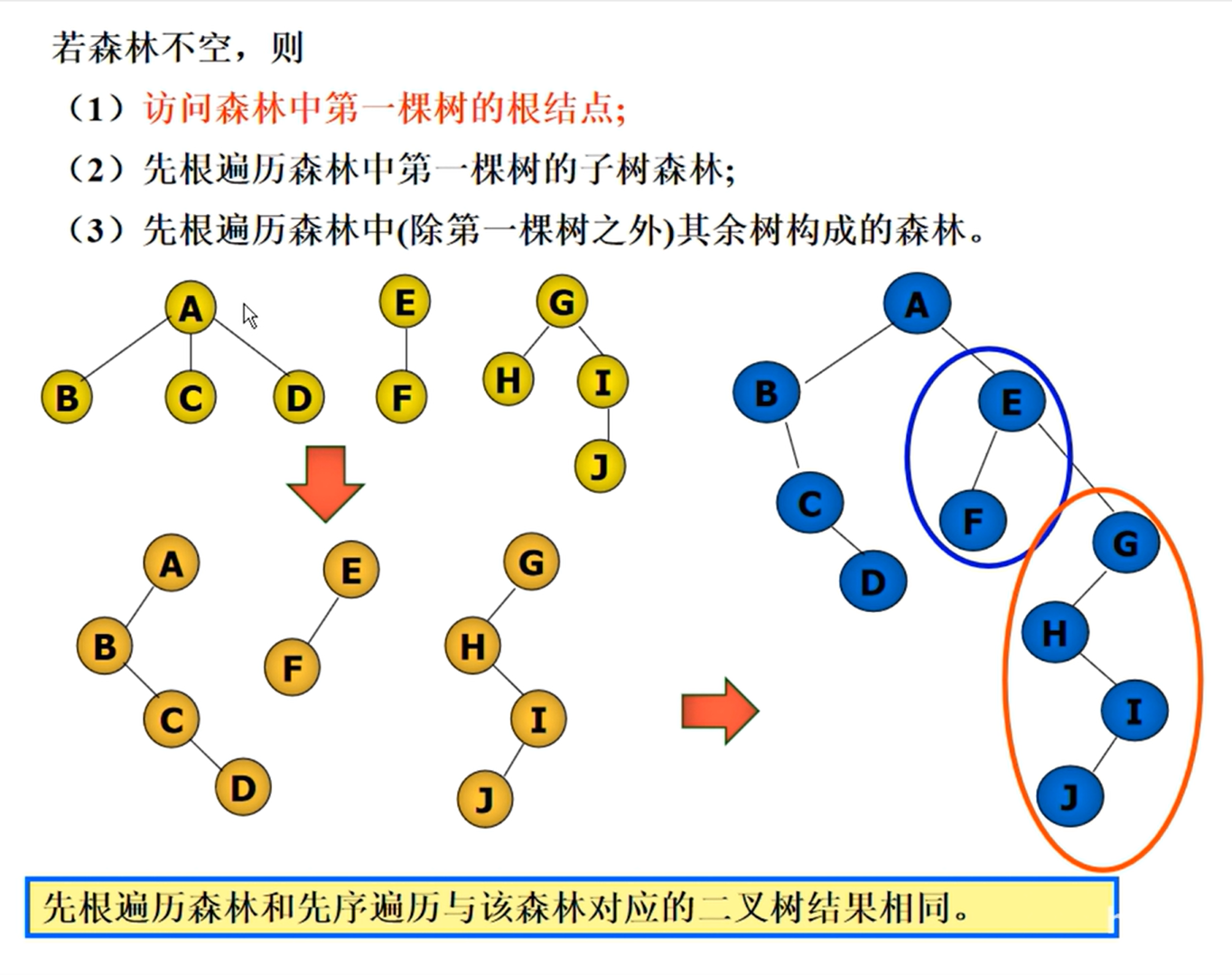
森林的遍历
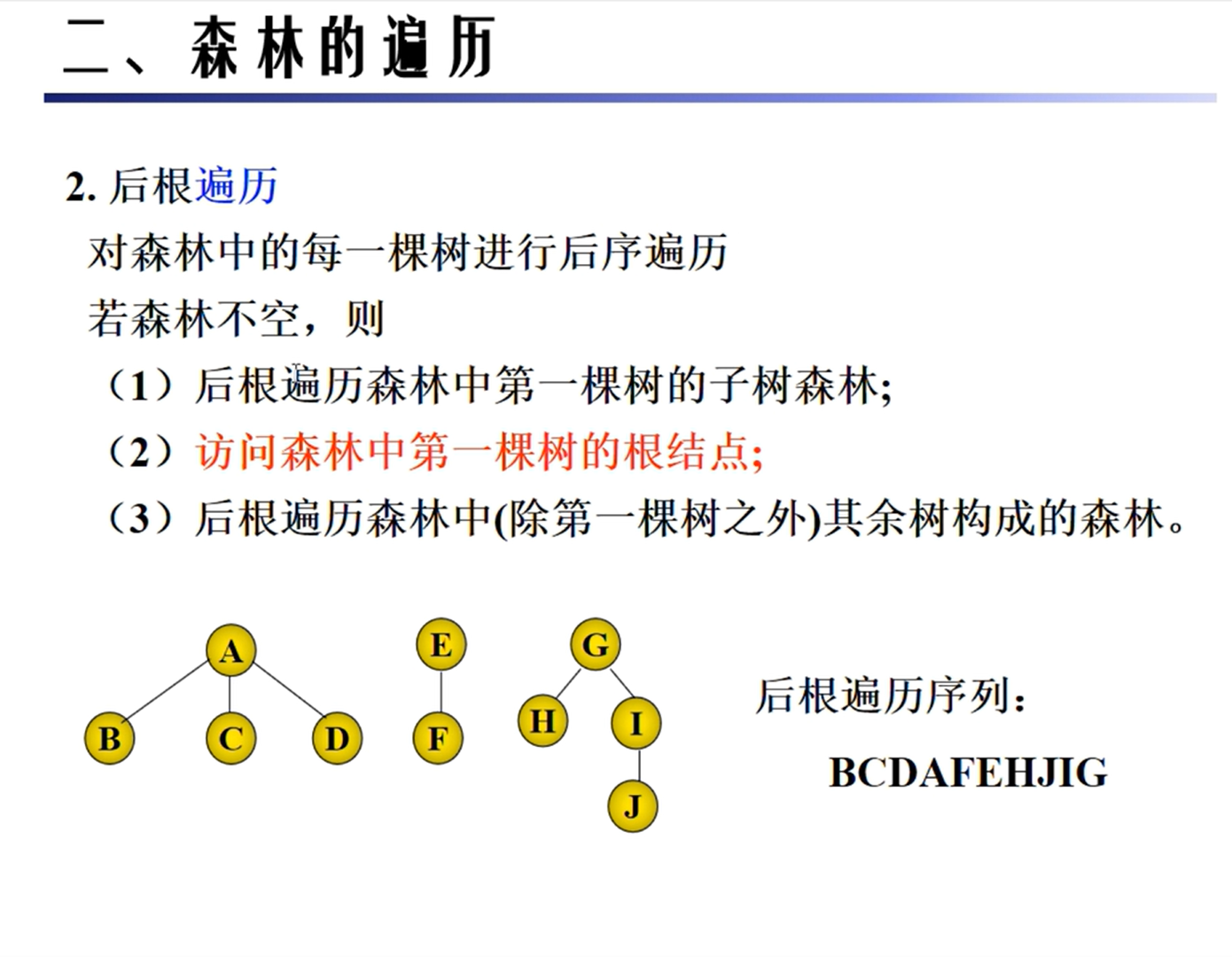
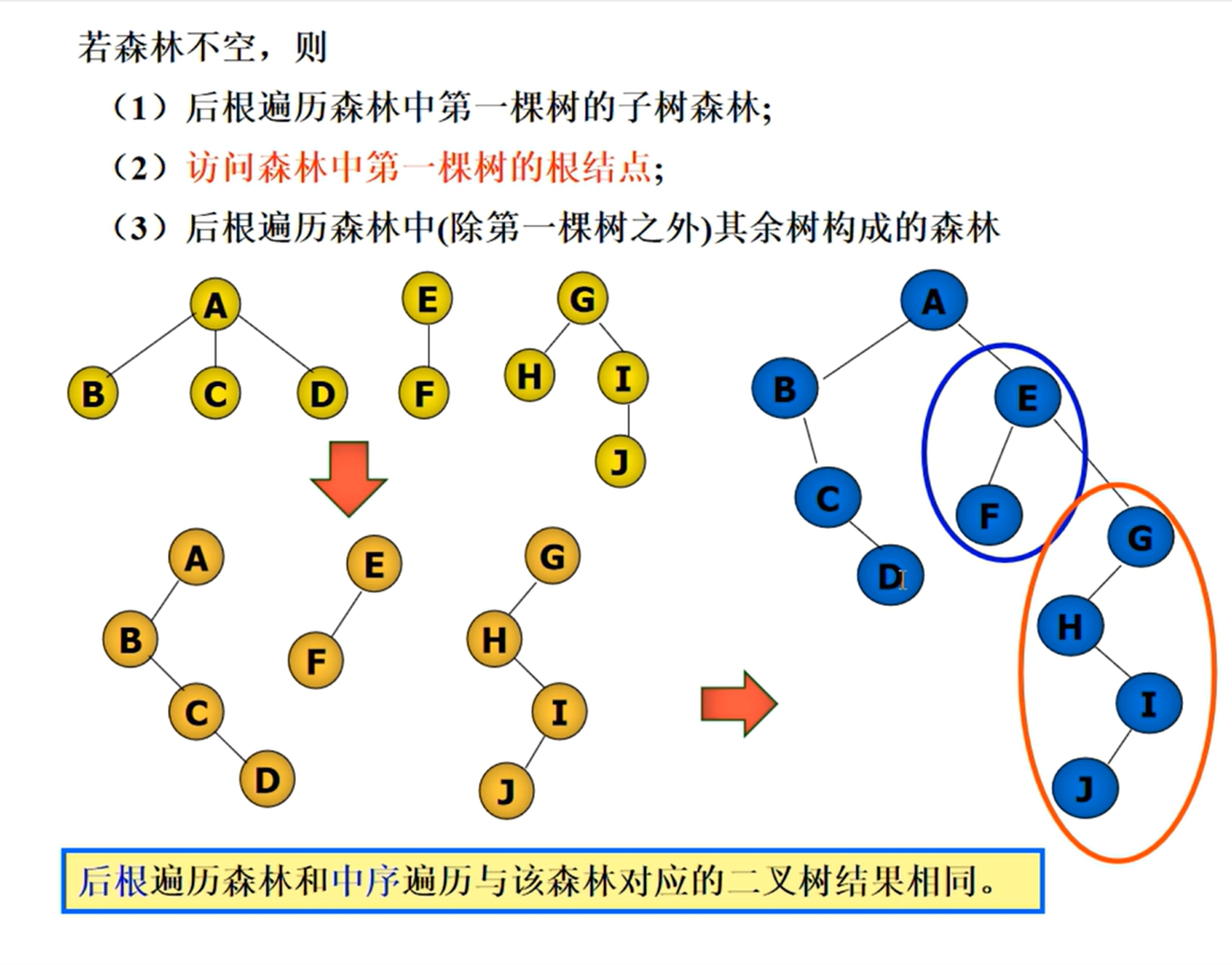
KMP匹配算法
1 | class Solution: |
图
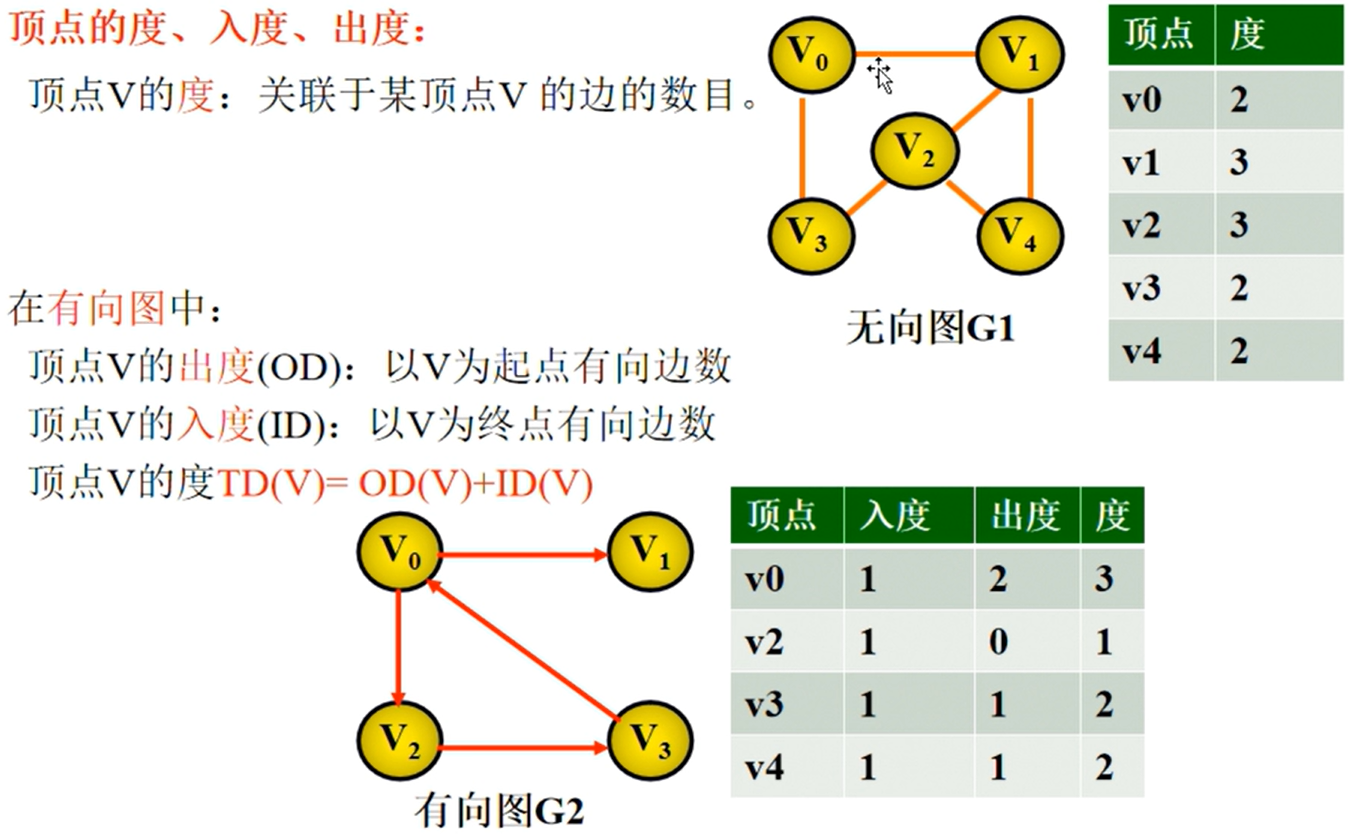
基本概念
图的定义
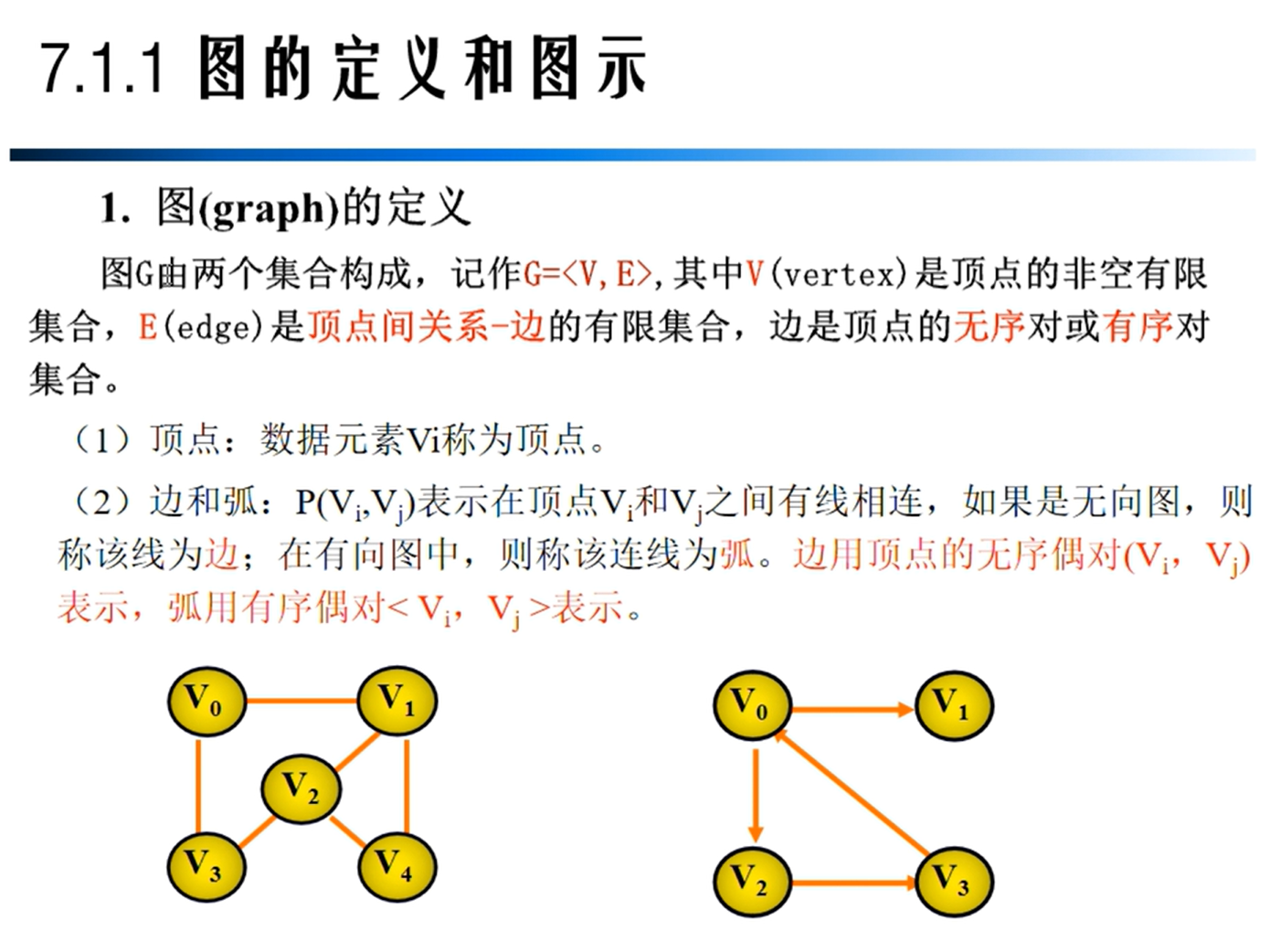

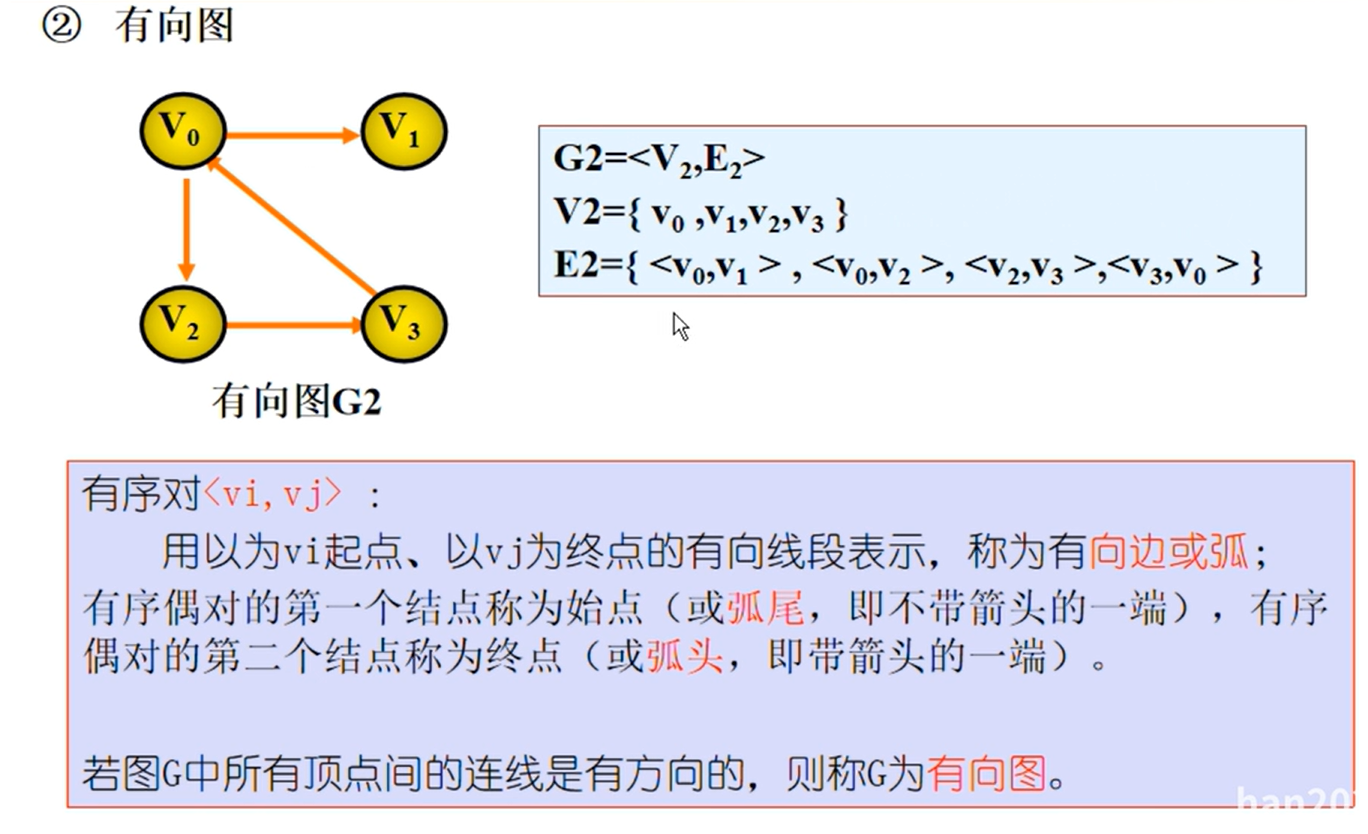
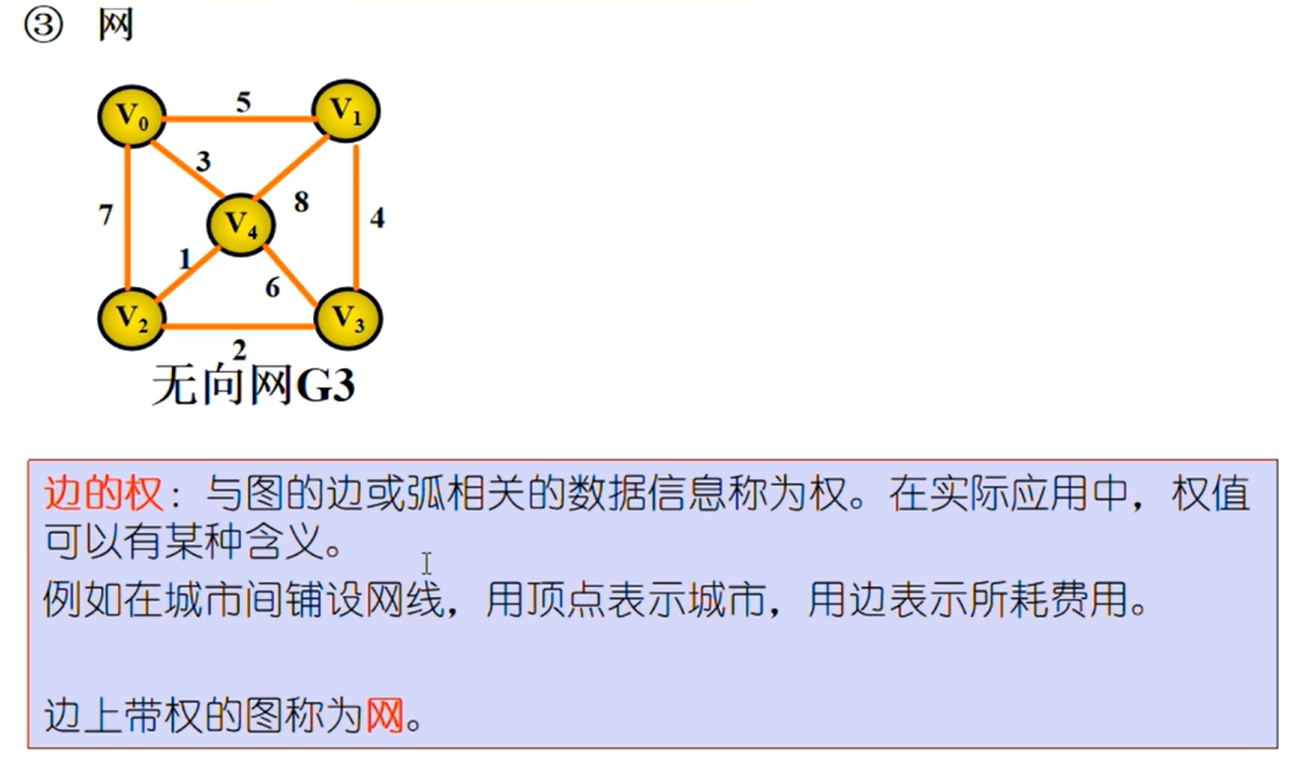
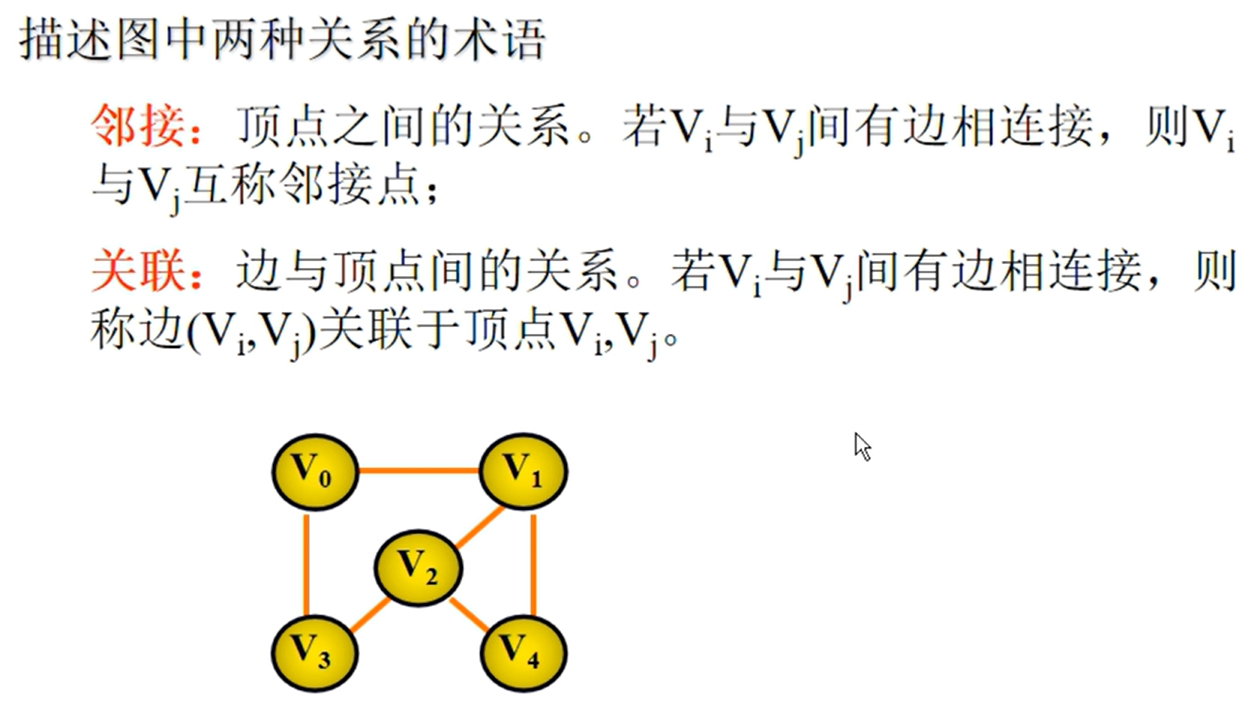
图的相关概念
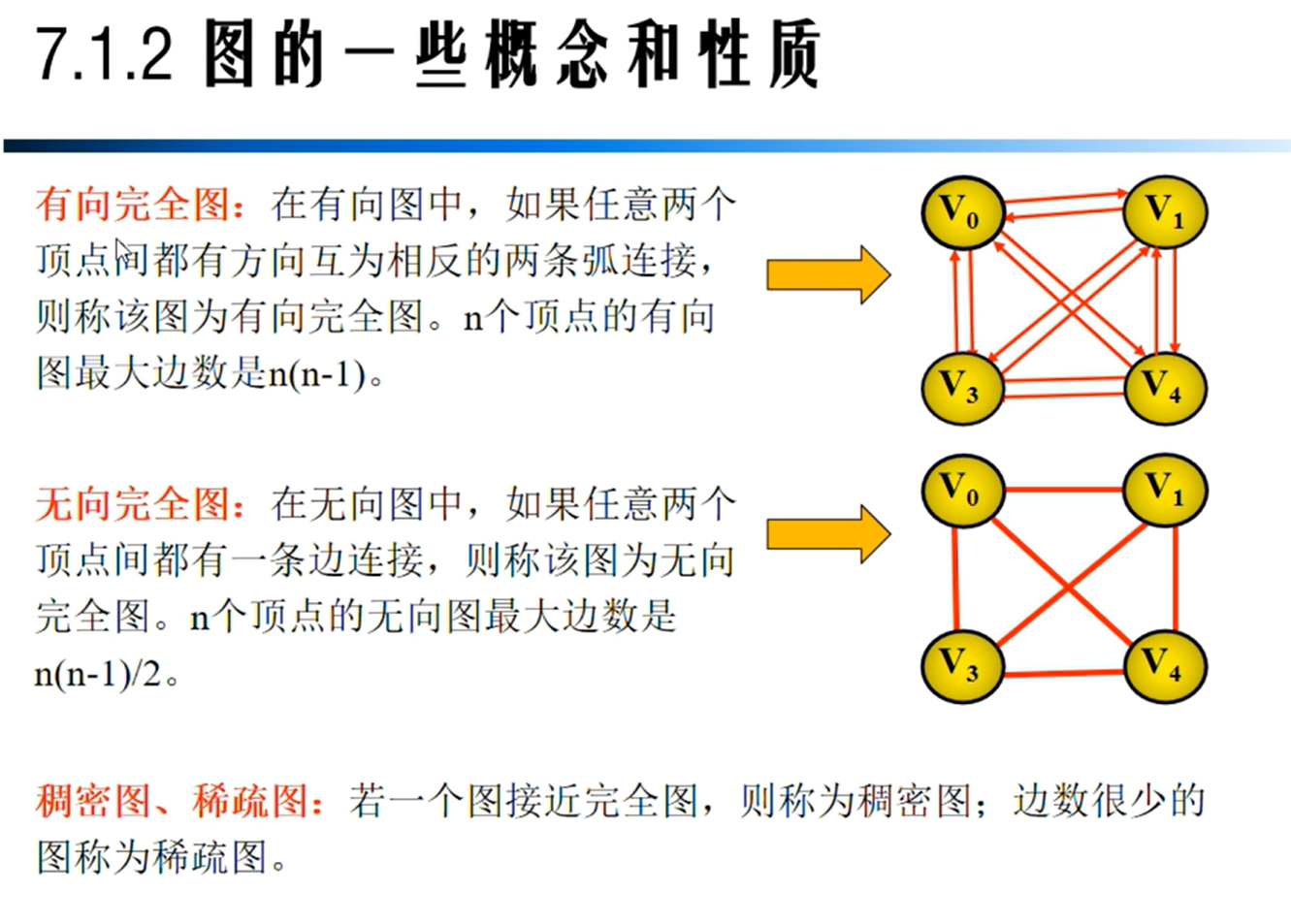


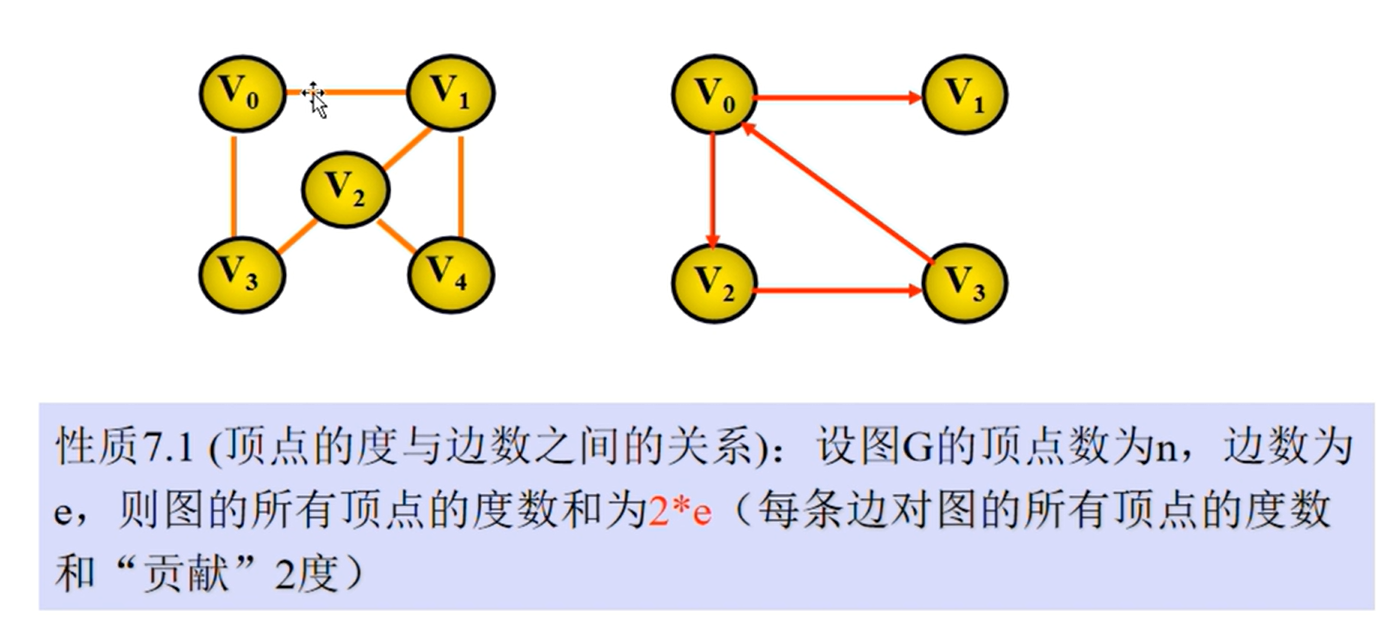
图的相关性质
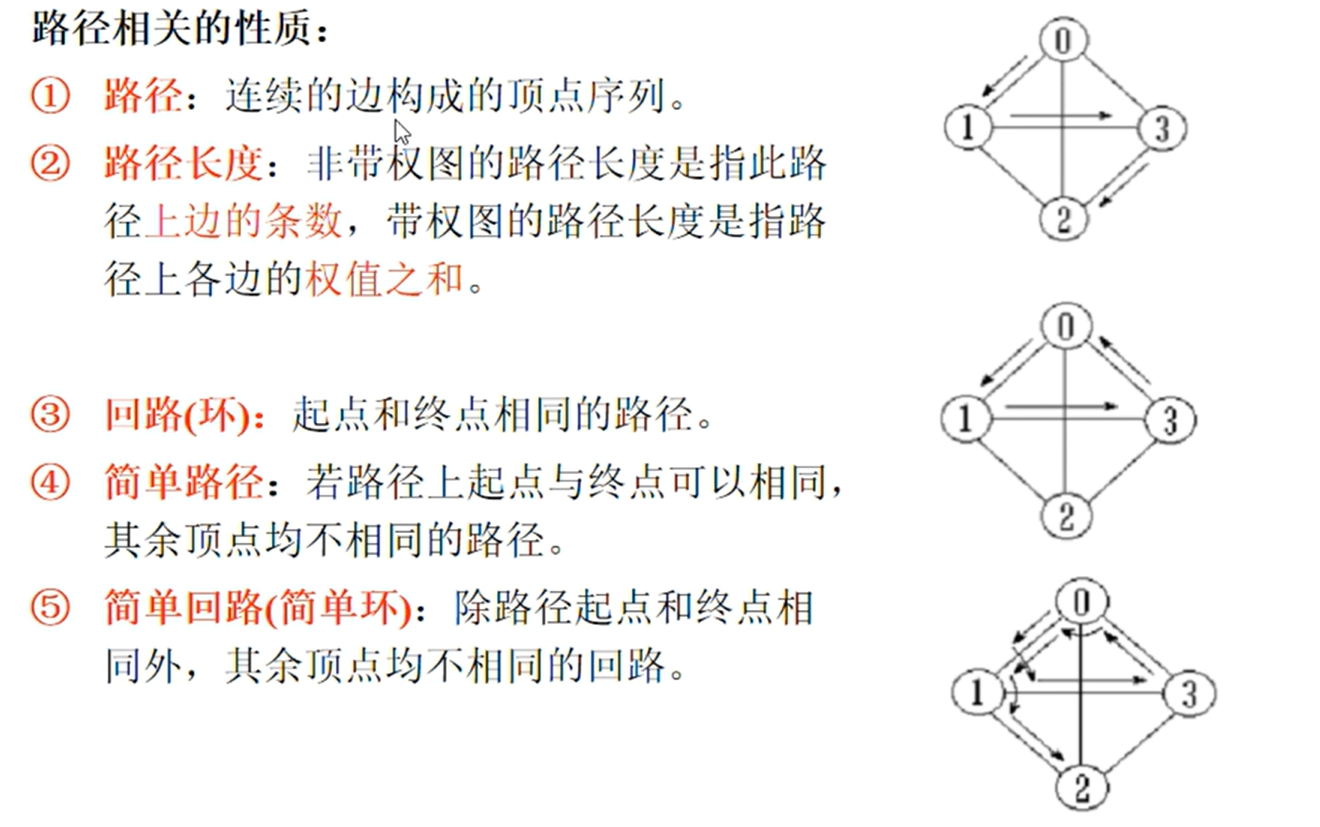
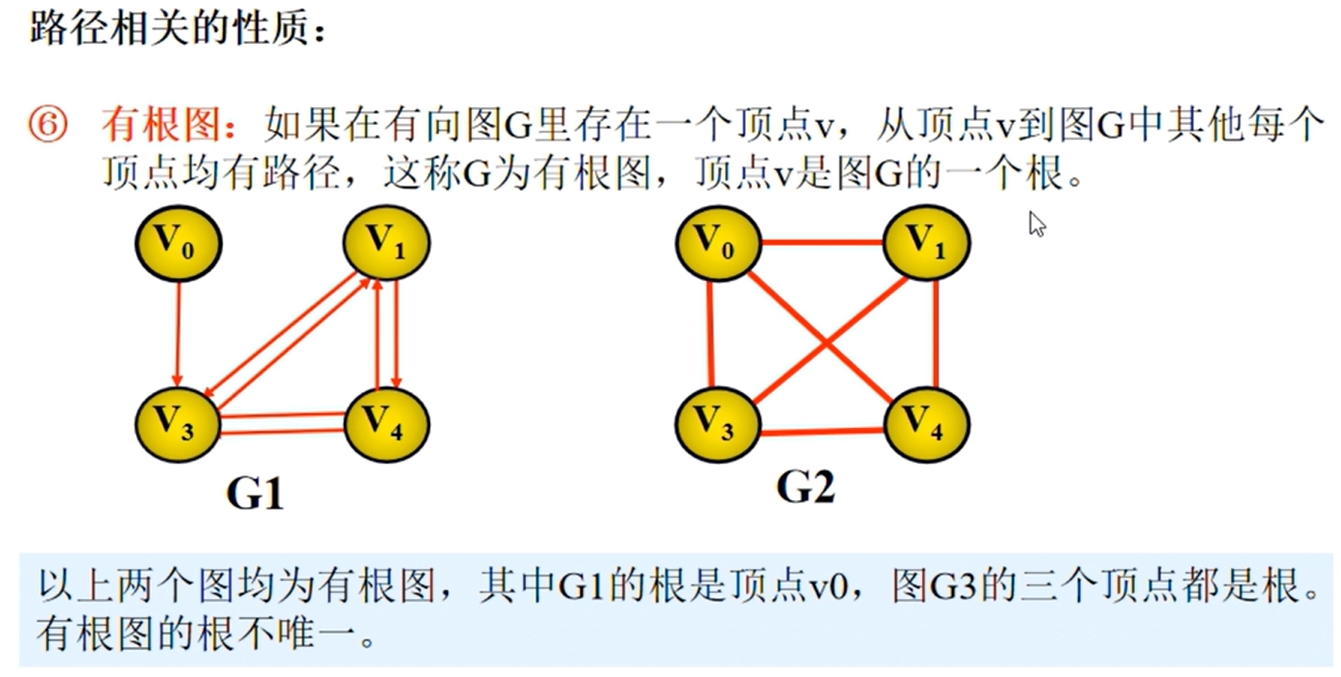

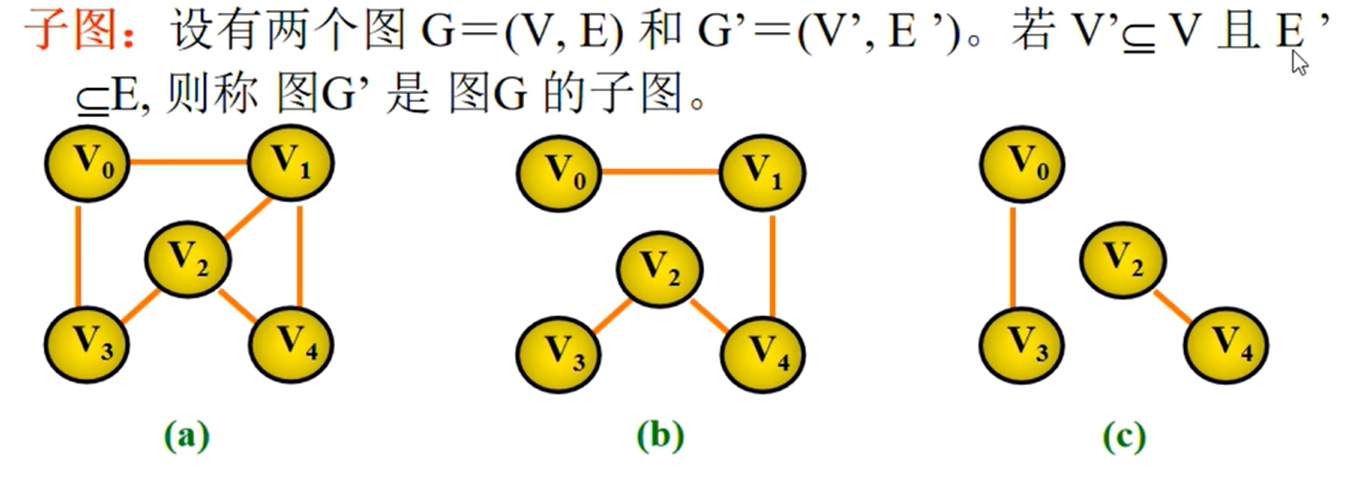
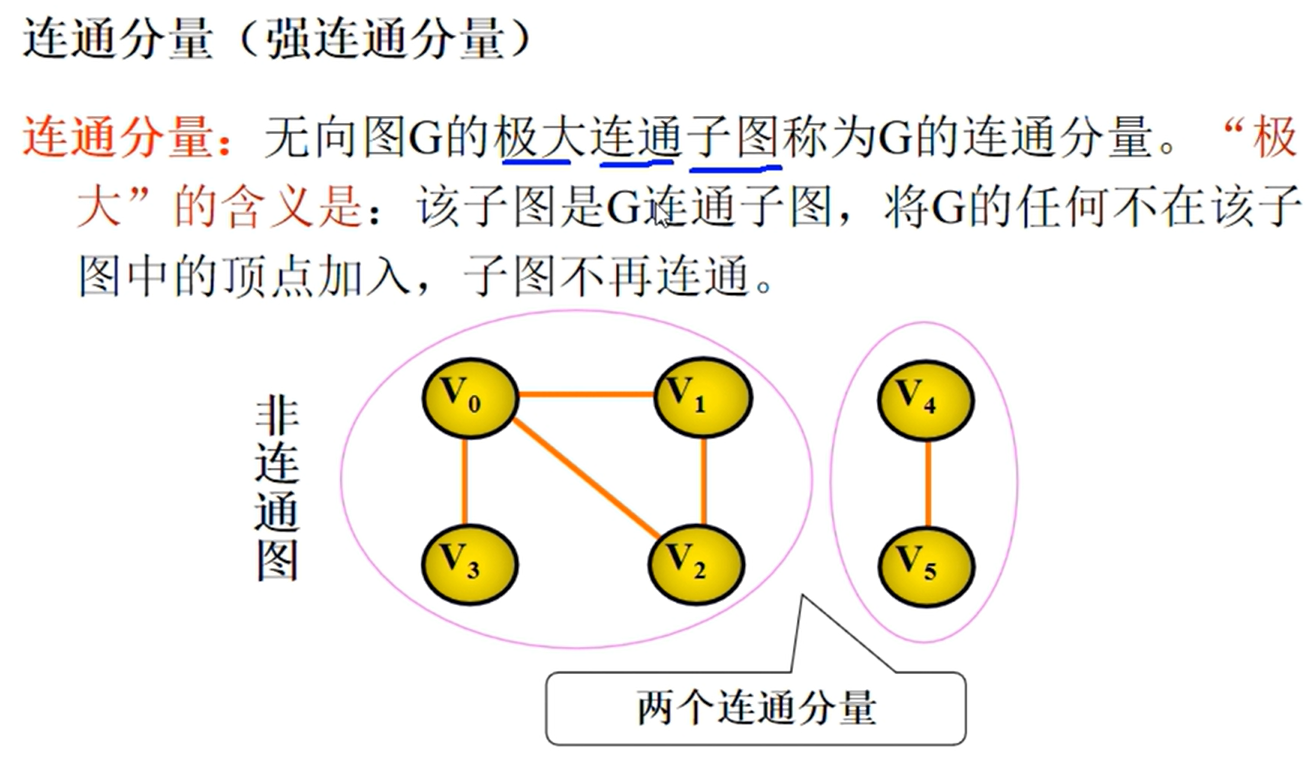
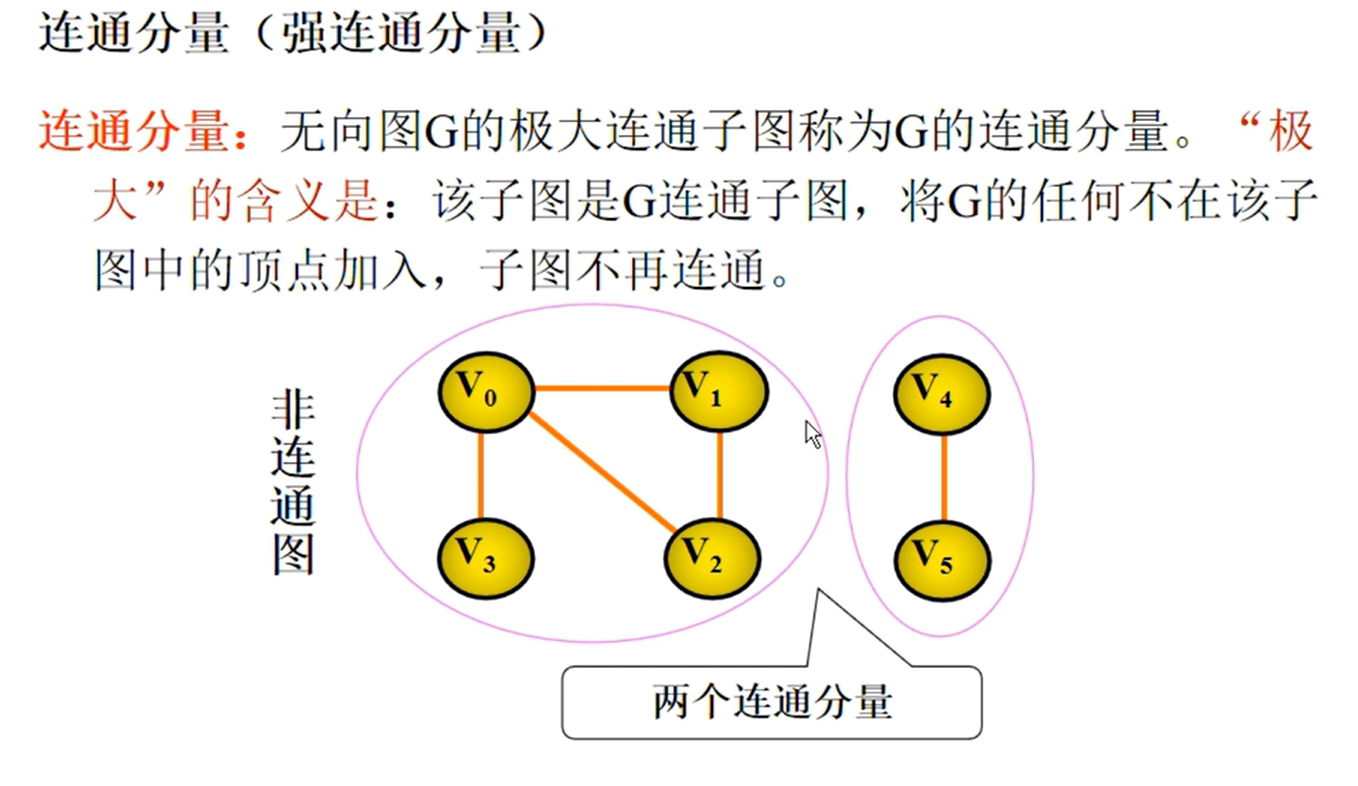
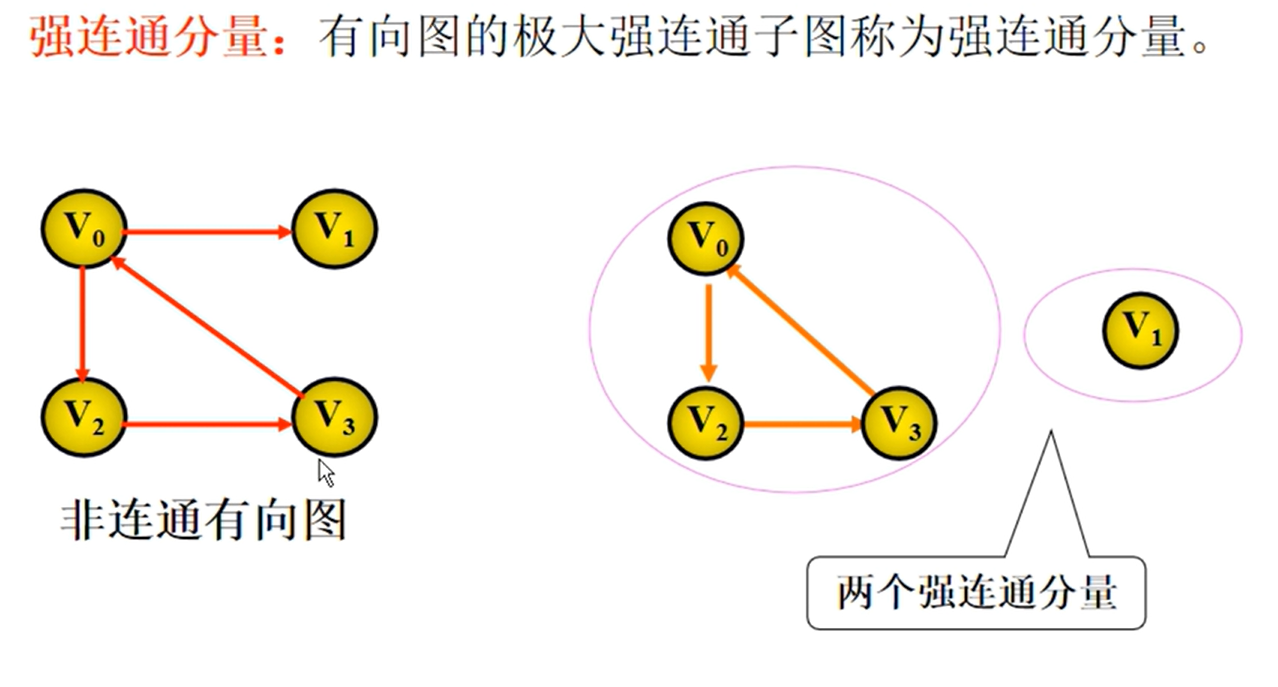
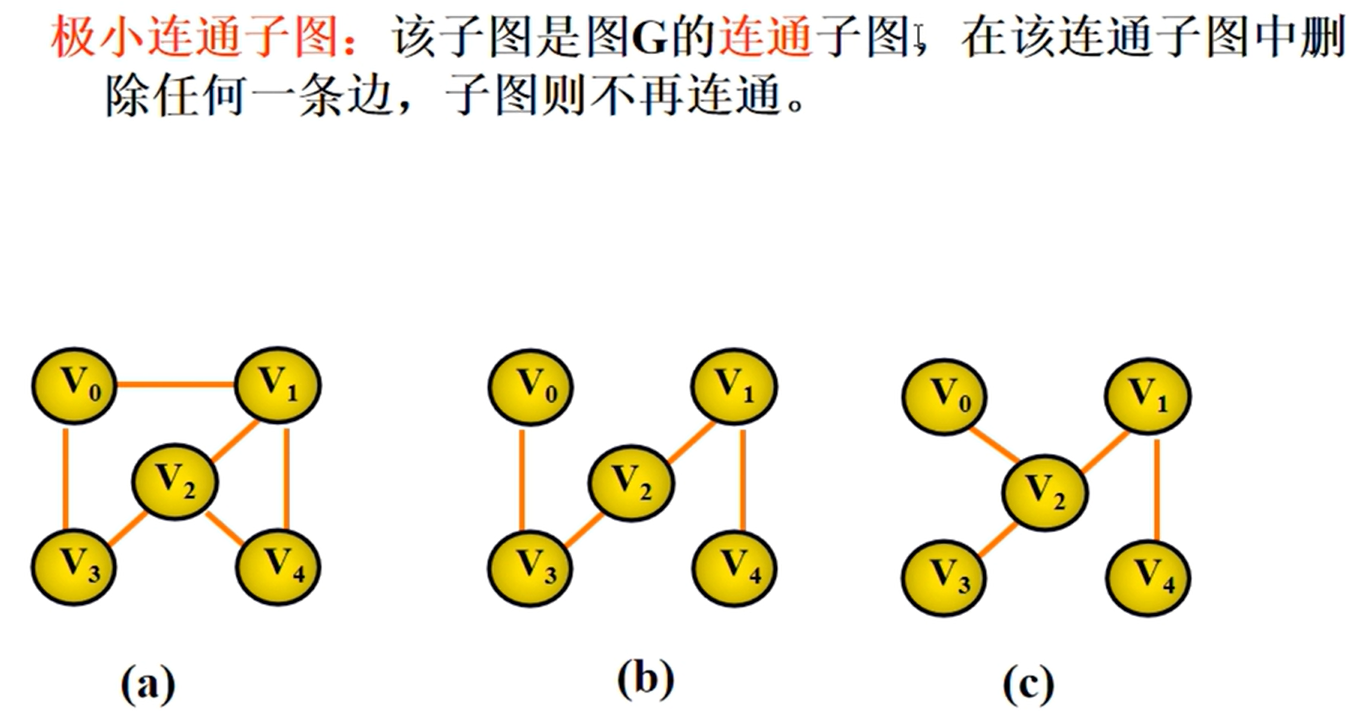
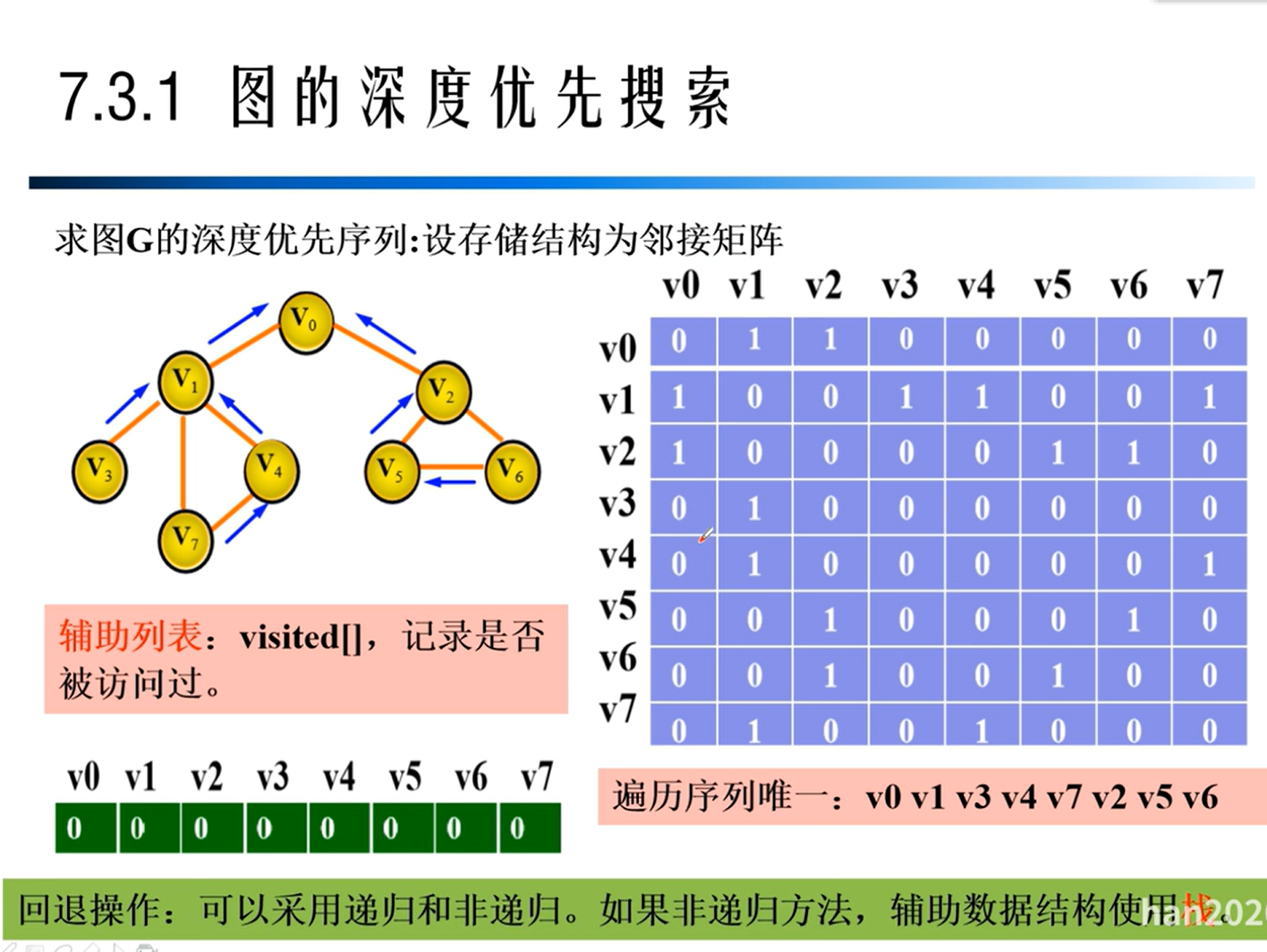
邻接矩阵
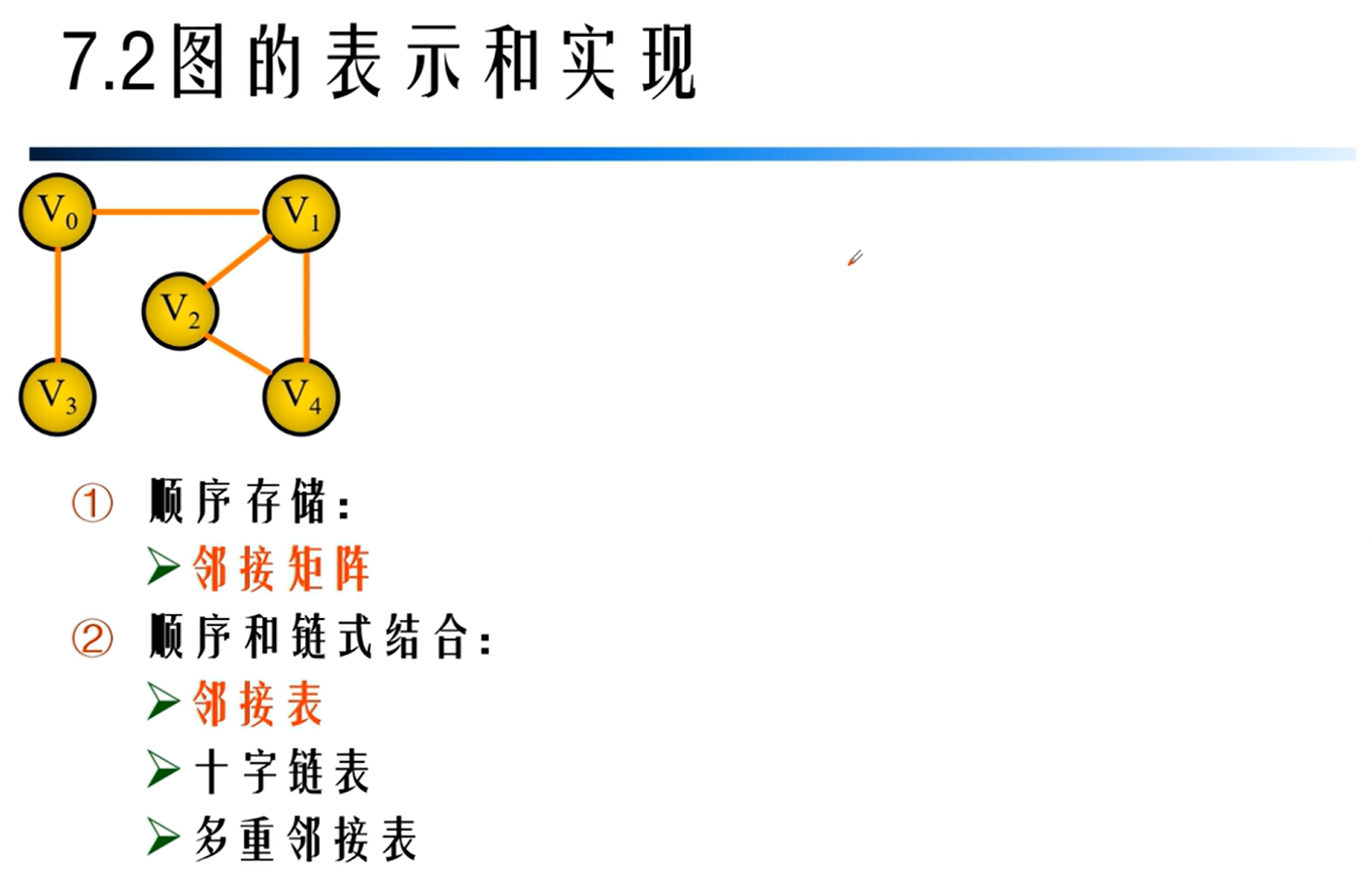

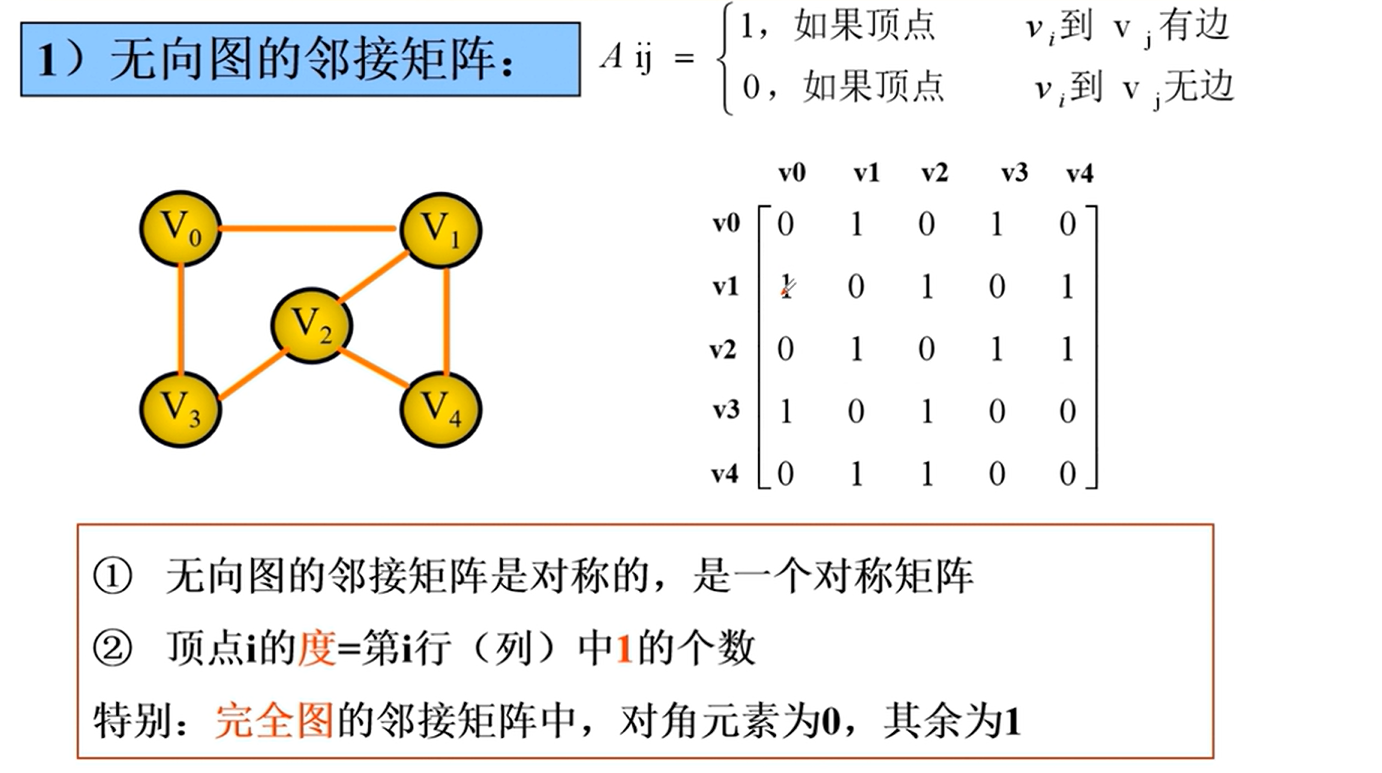
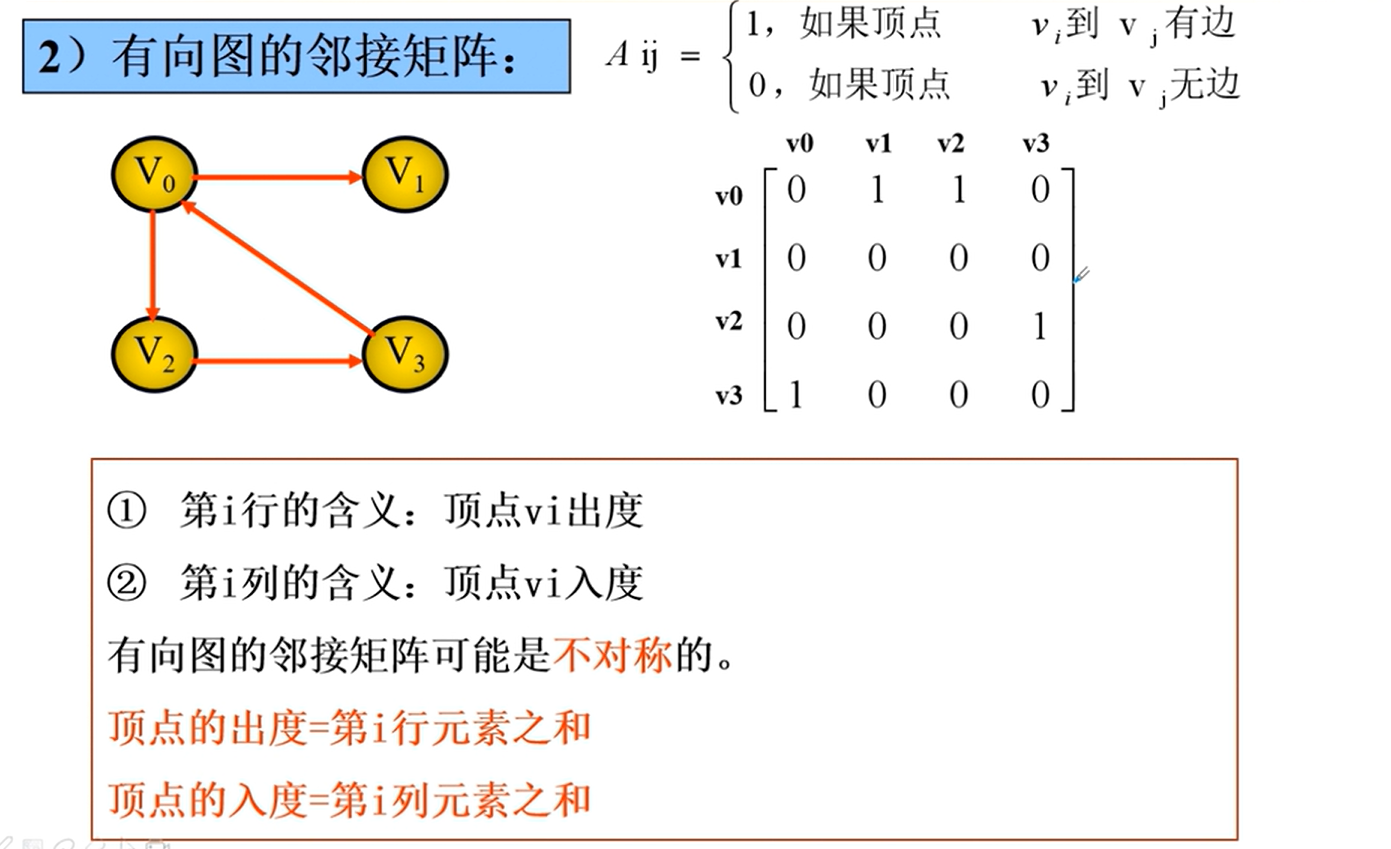
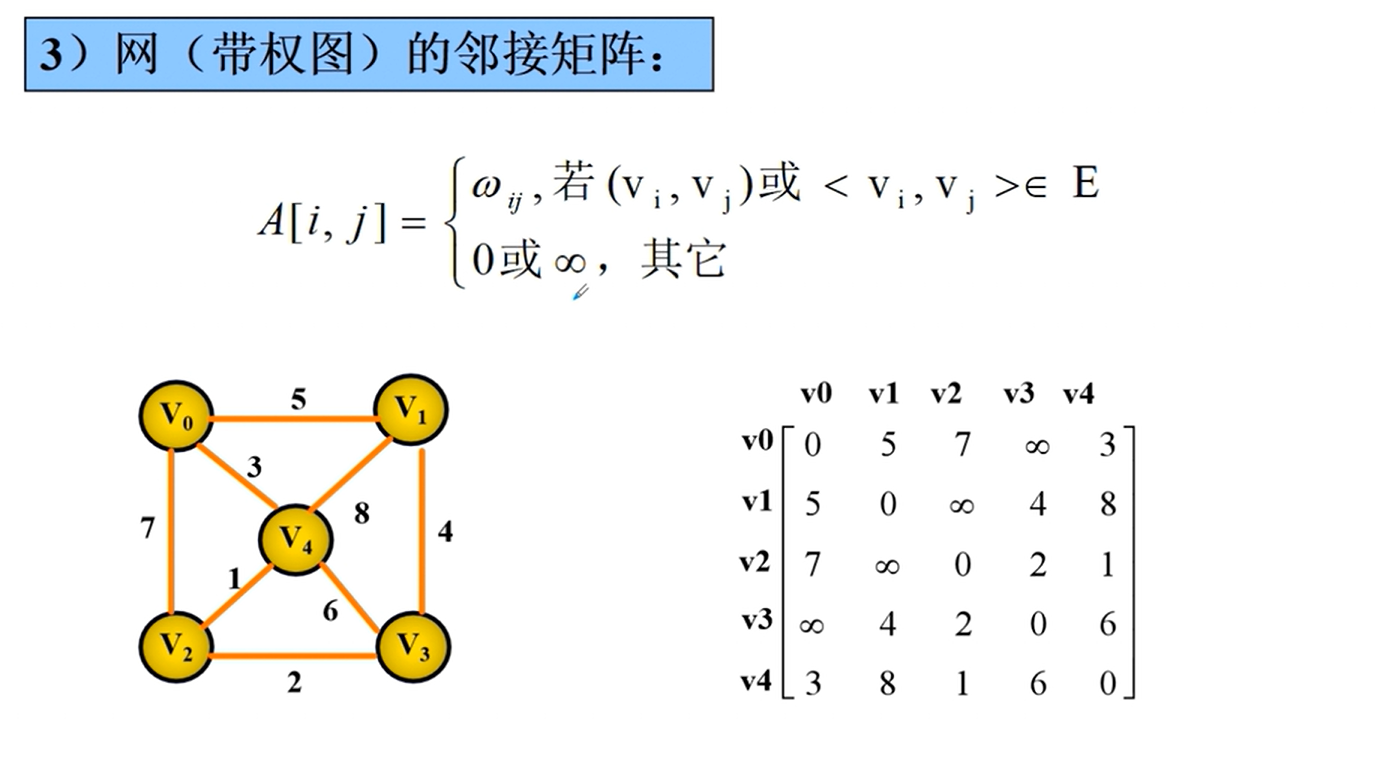
邻接矩阵的实现


邻接矩阵的优劣


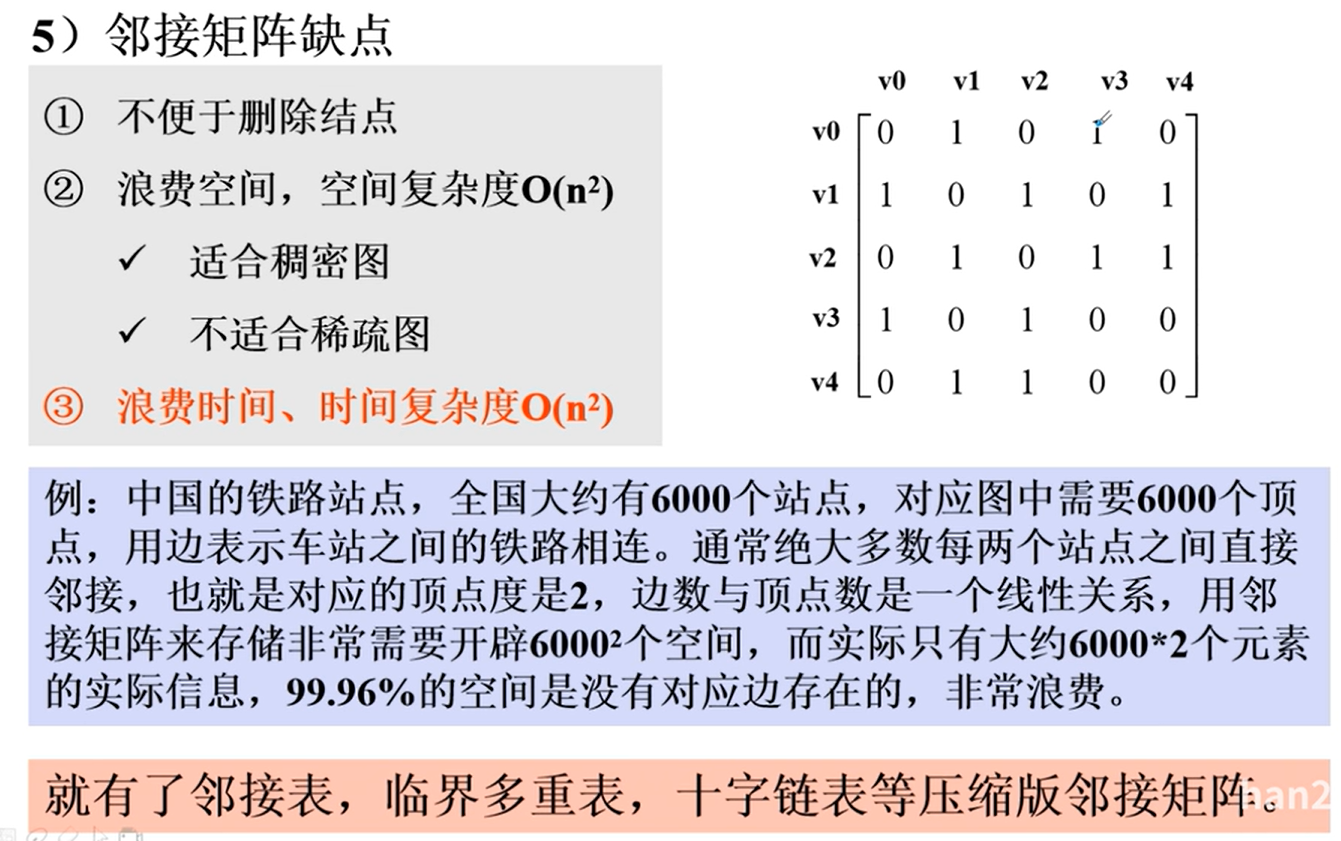
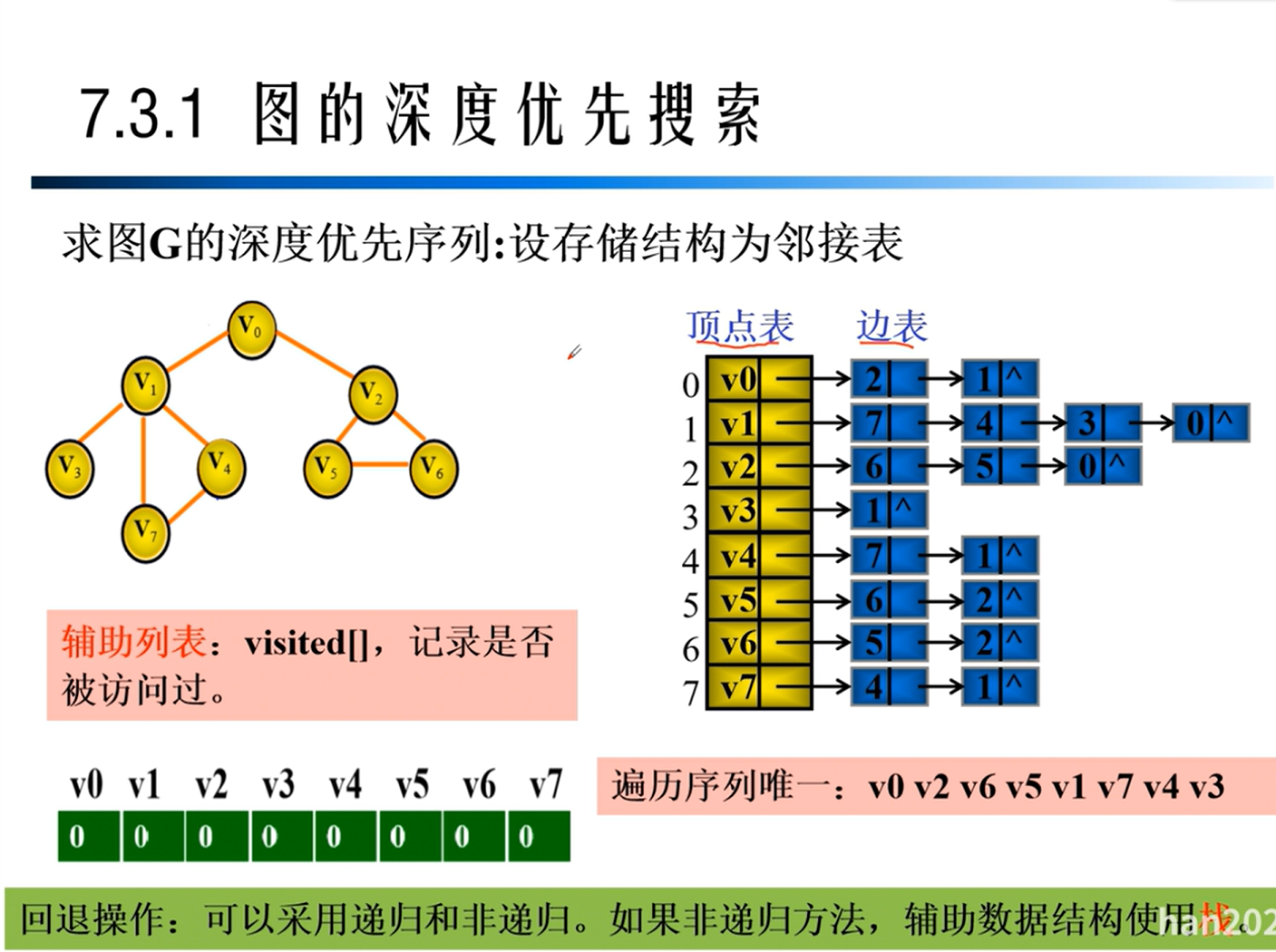
邻接表
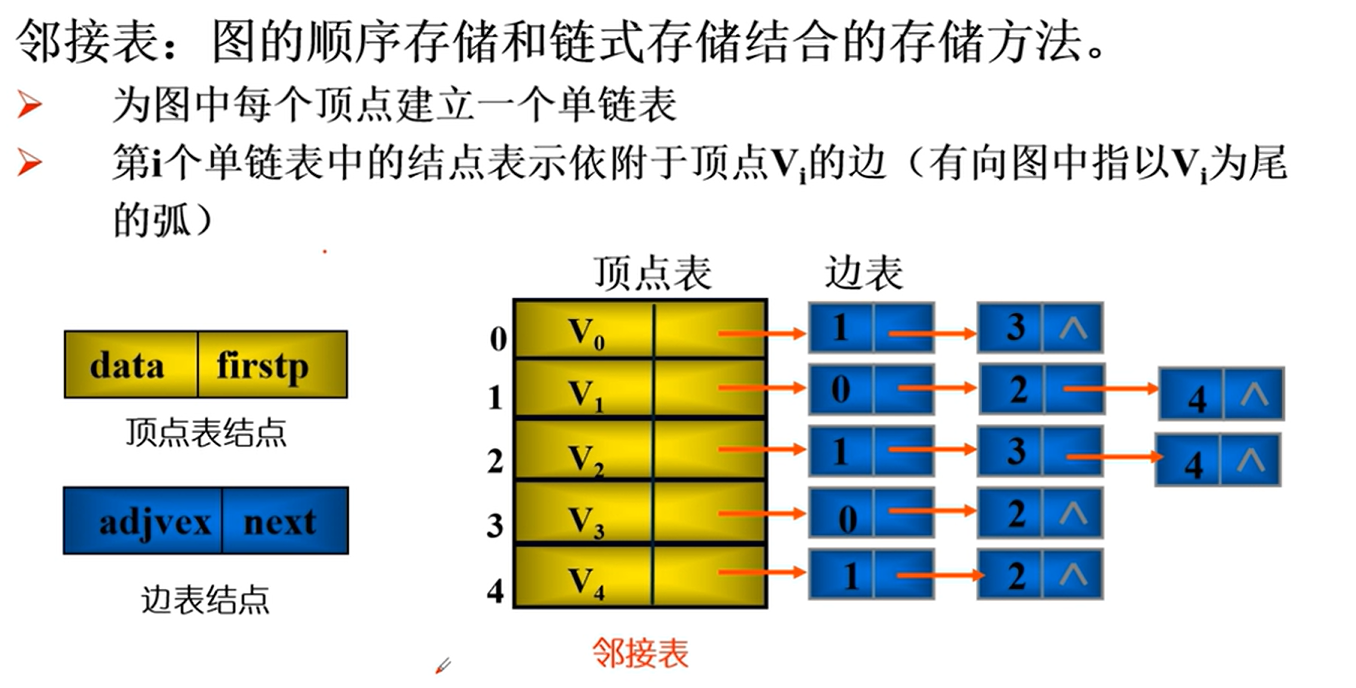

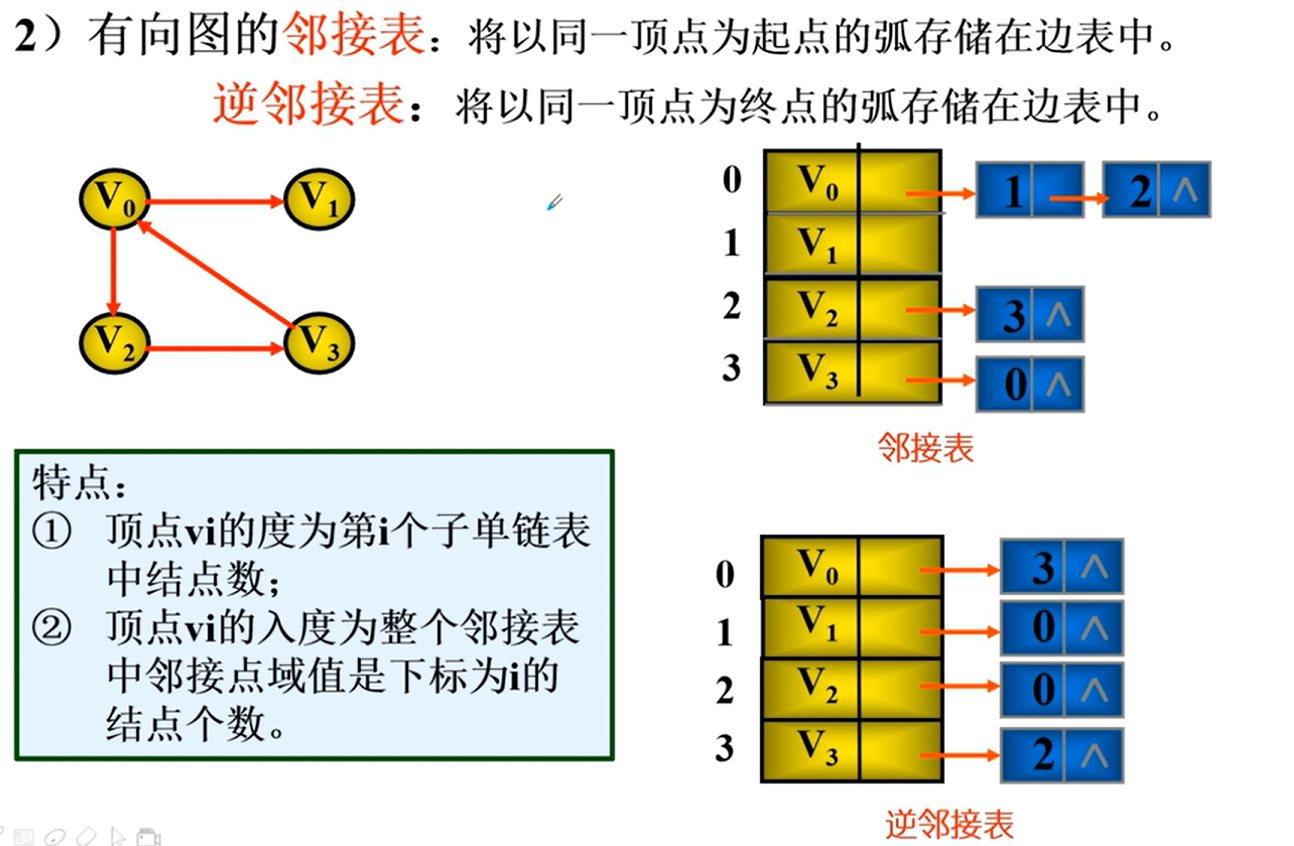
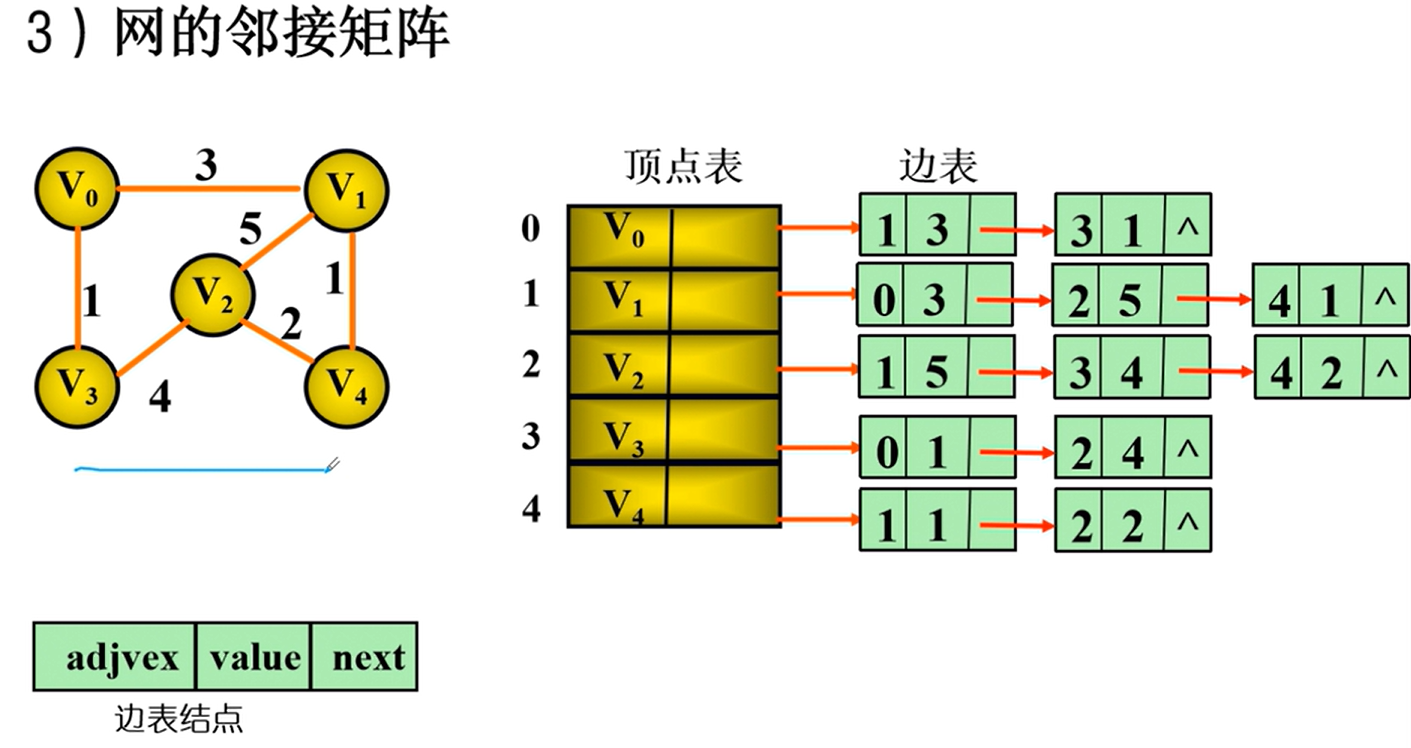
邻接表的实现



特点

库的调用

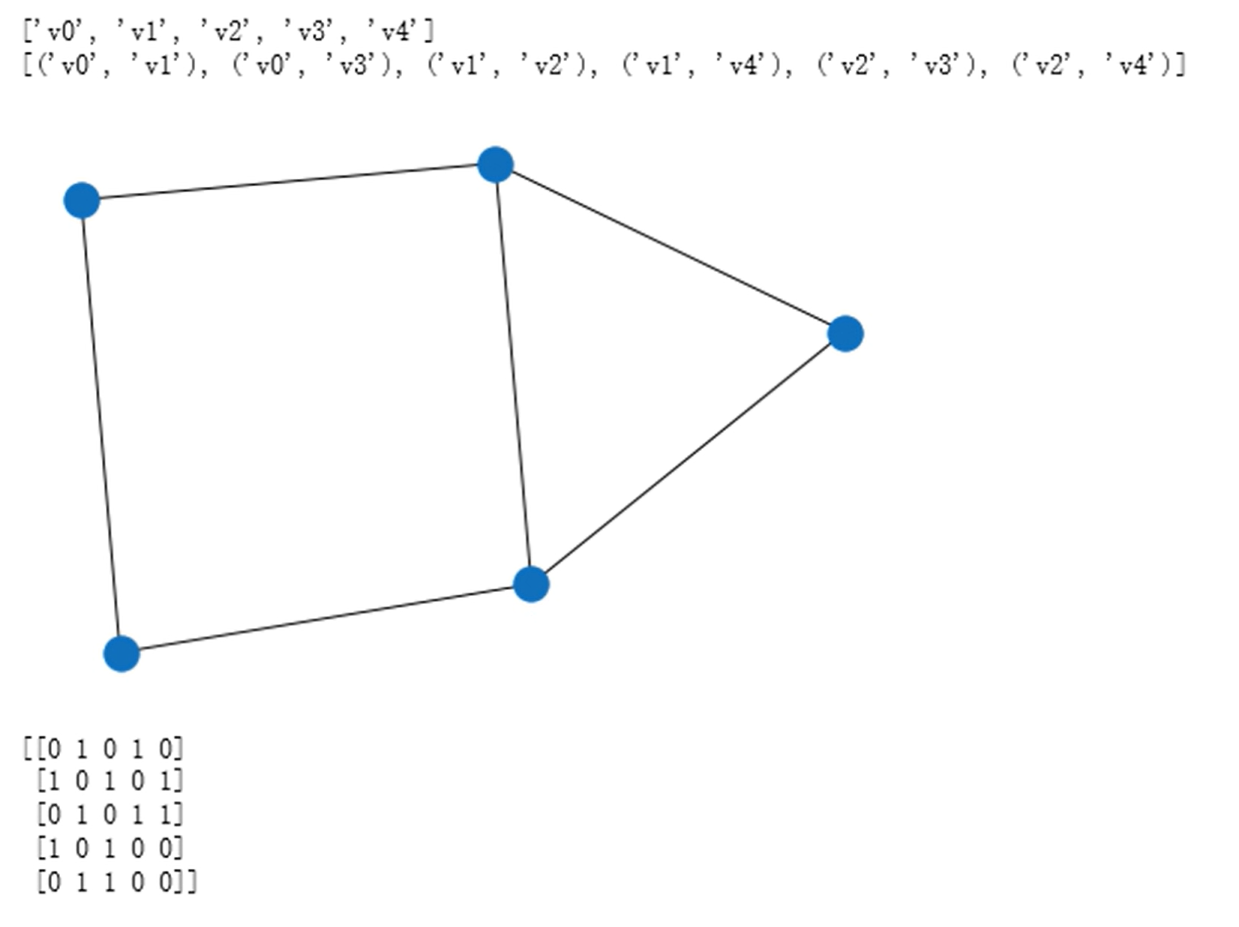
图的遍历

深度优先遍历
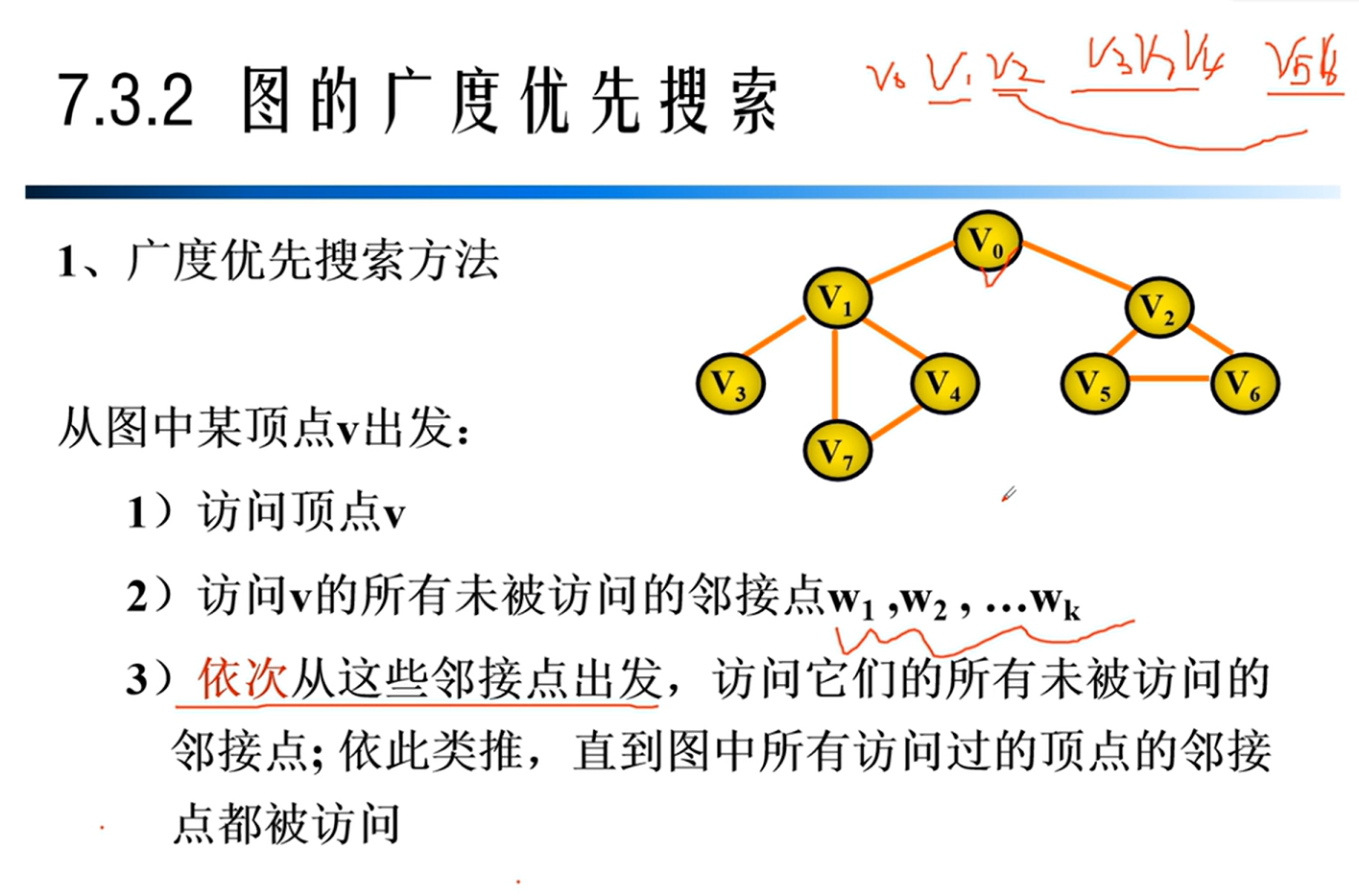
广度优先遍历
BFS与DFS算法比较
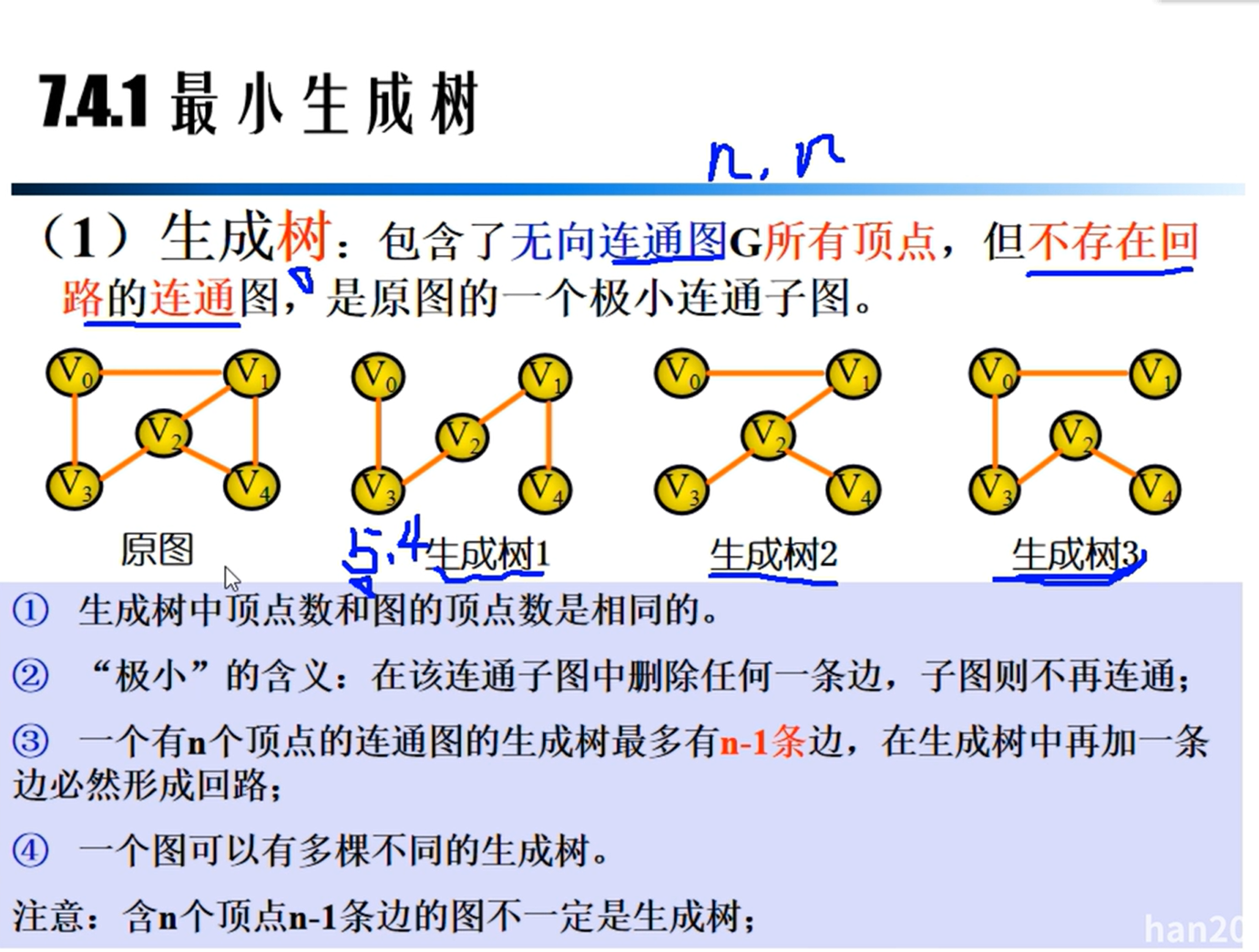
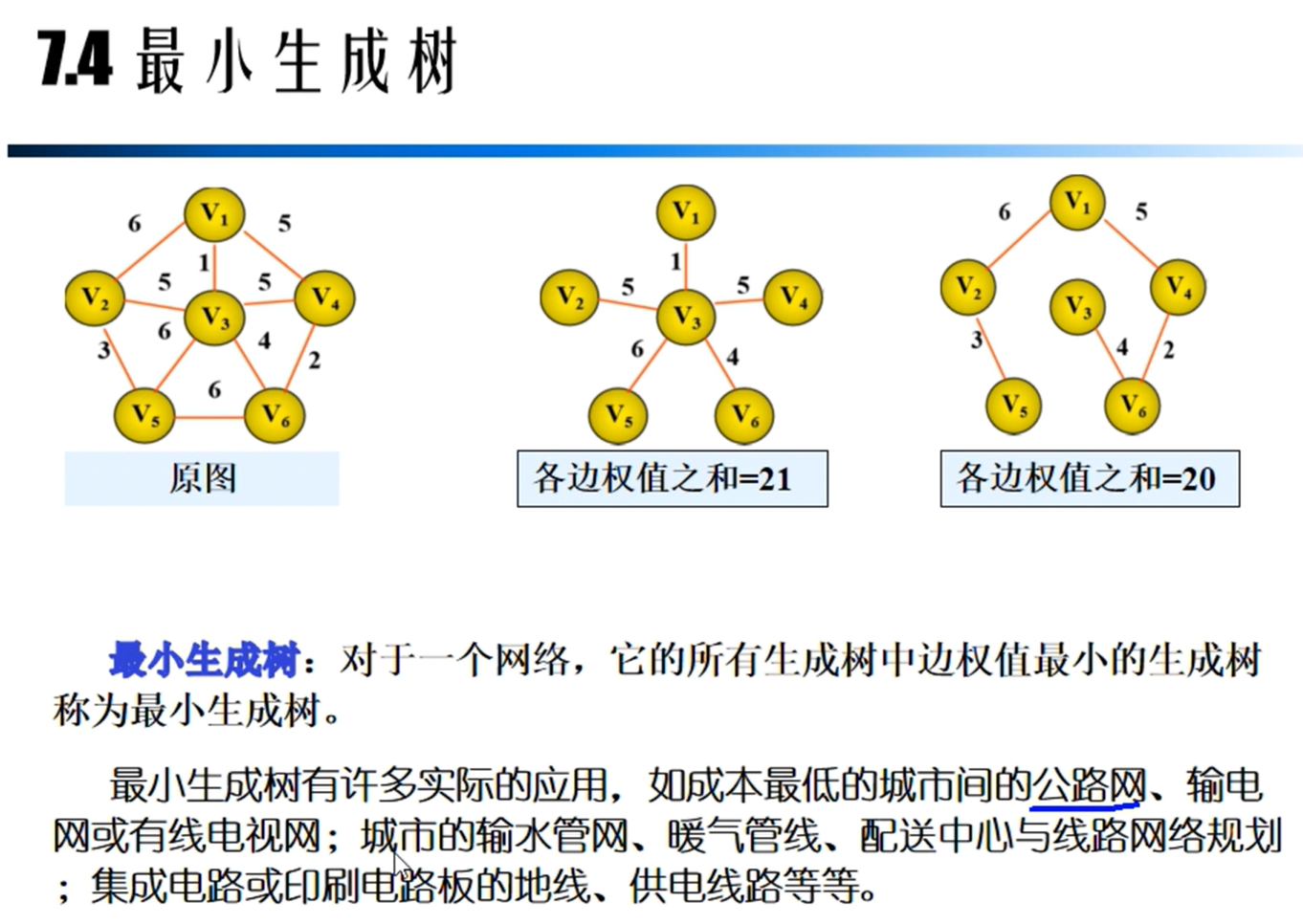
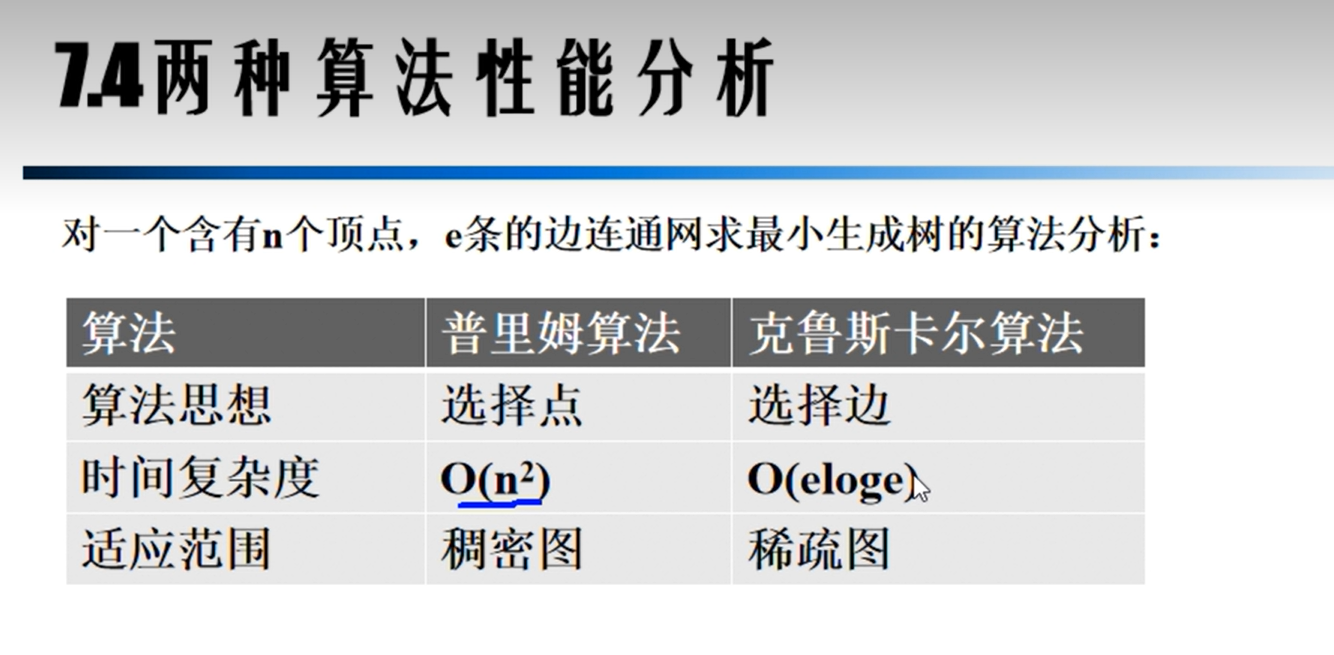
最小生成树
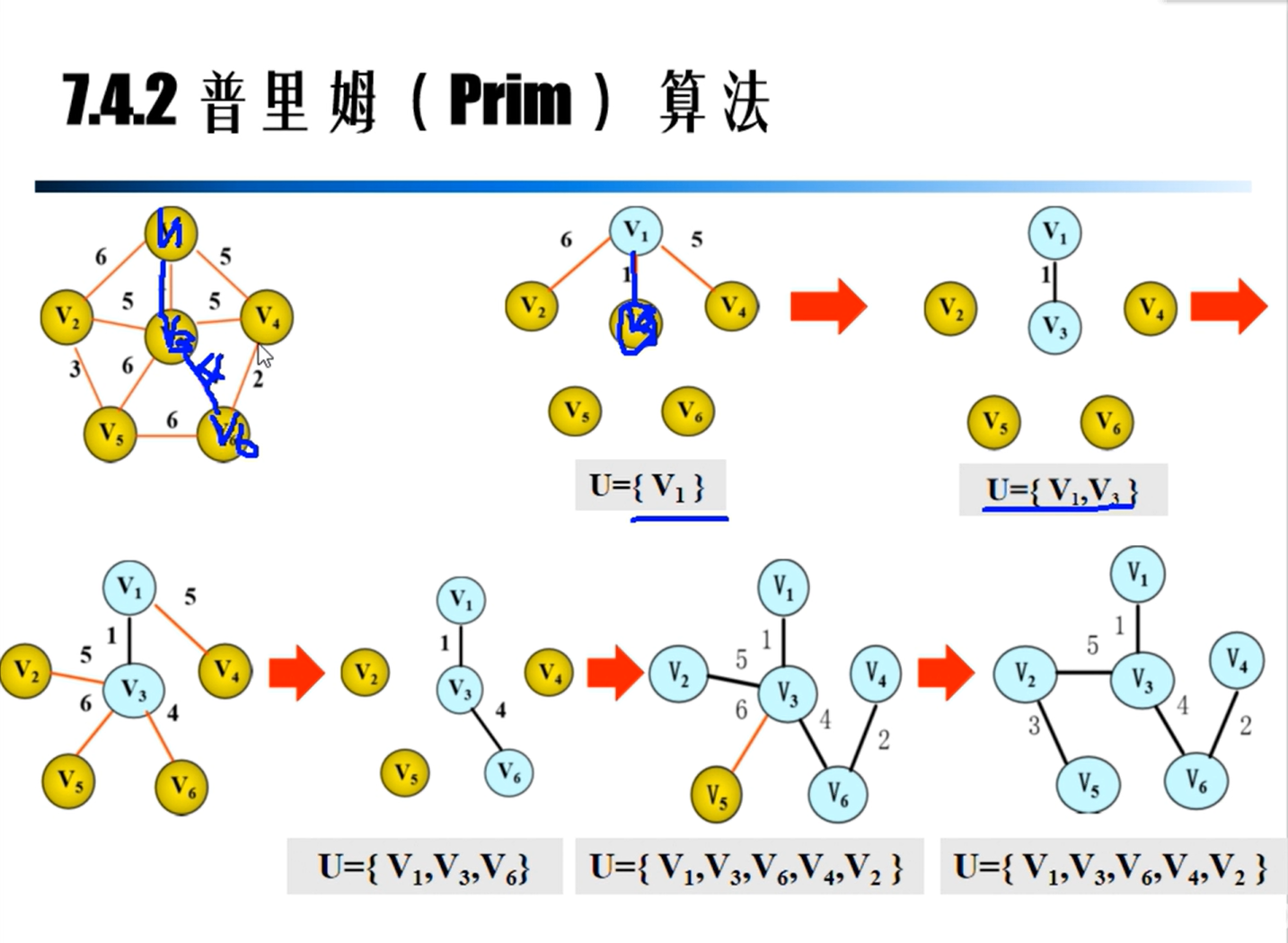
Prim算法
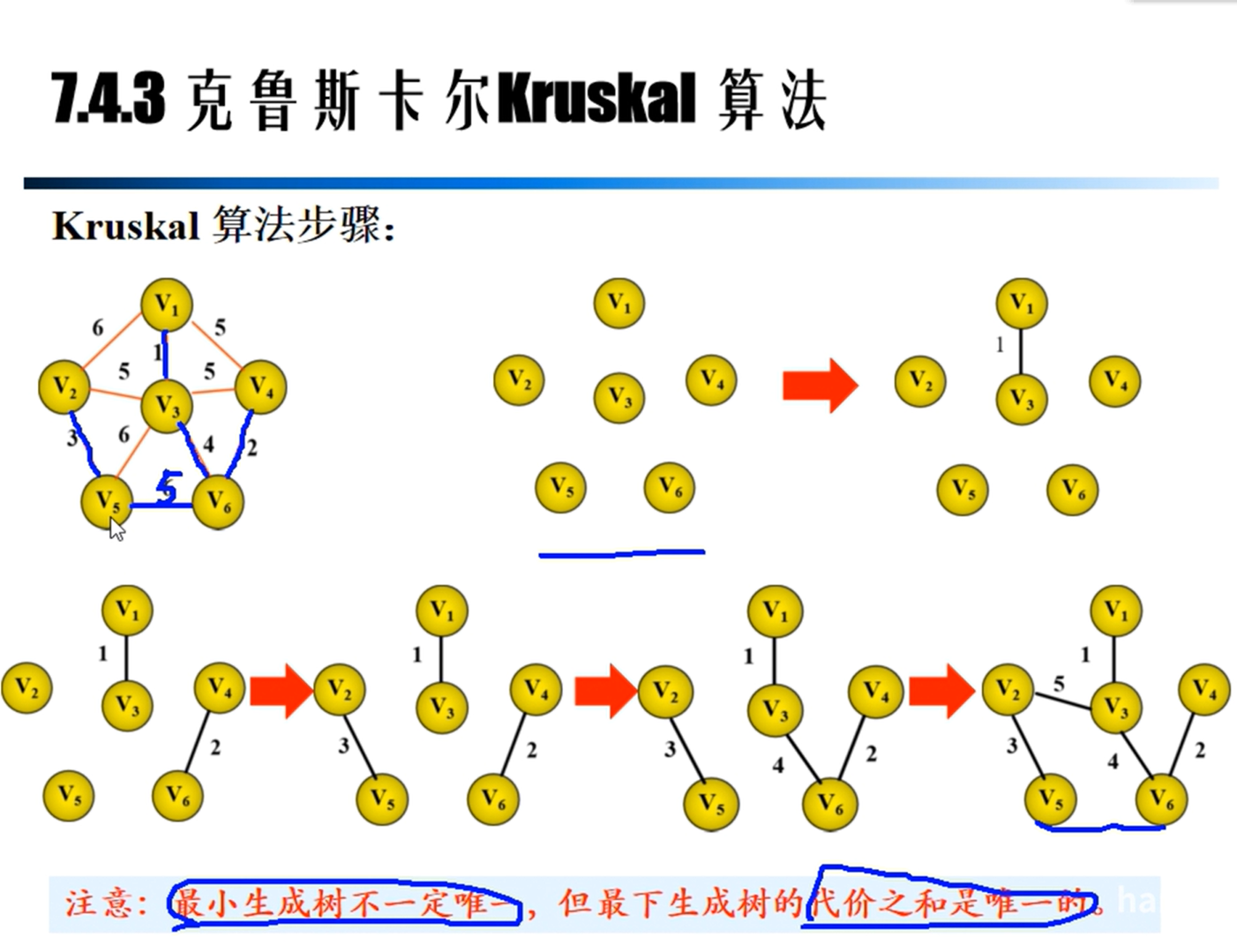
Kruskal算法
算法比较
最短路径
迪杰斯特拉算法
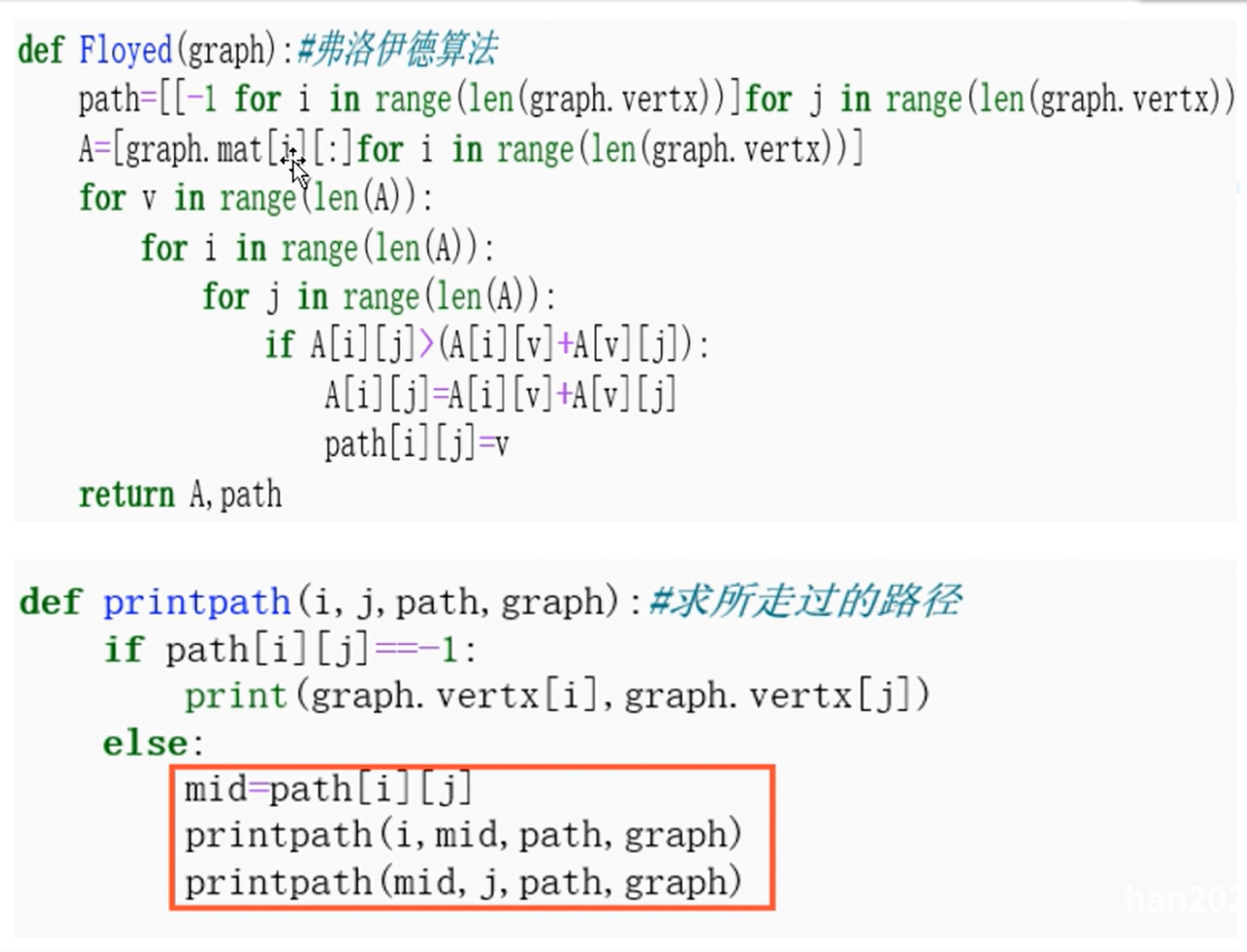
弗洛伊德算法
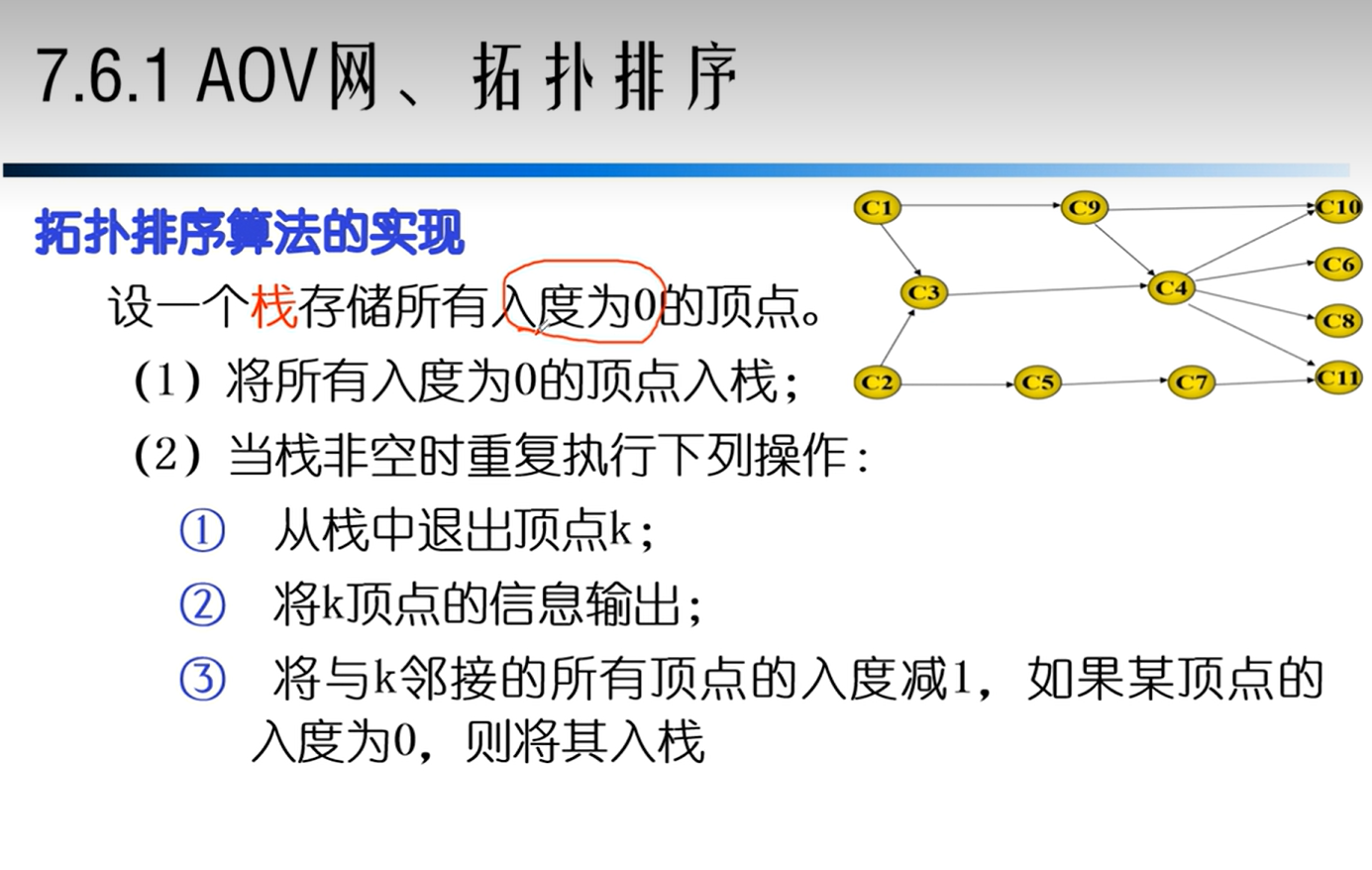
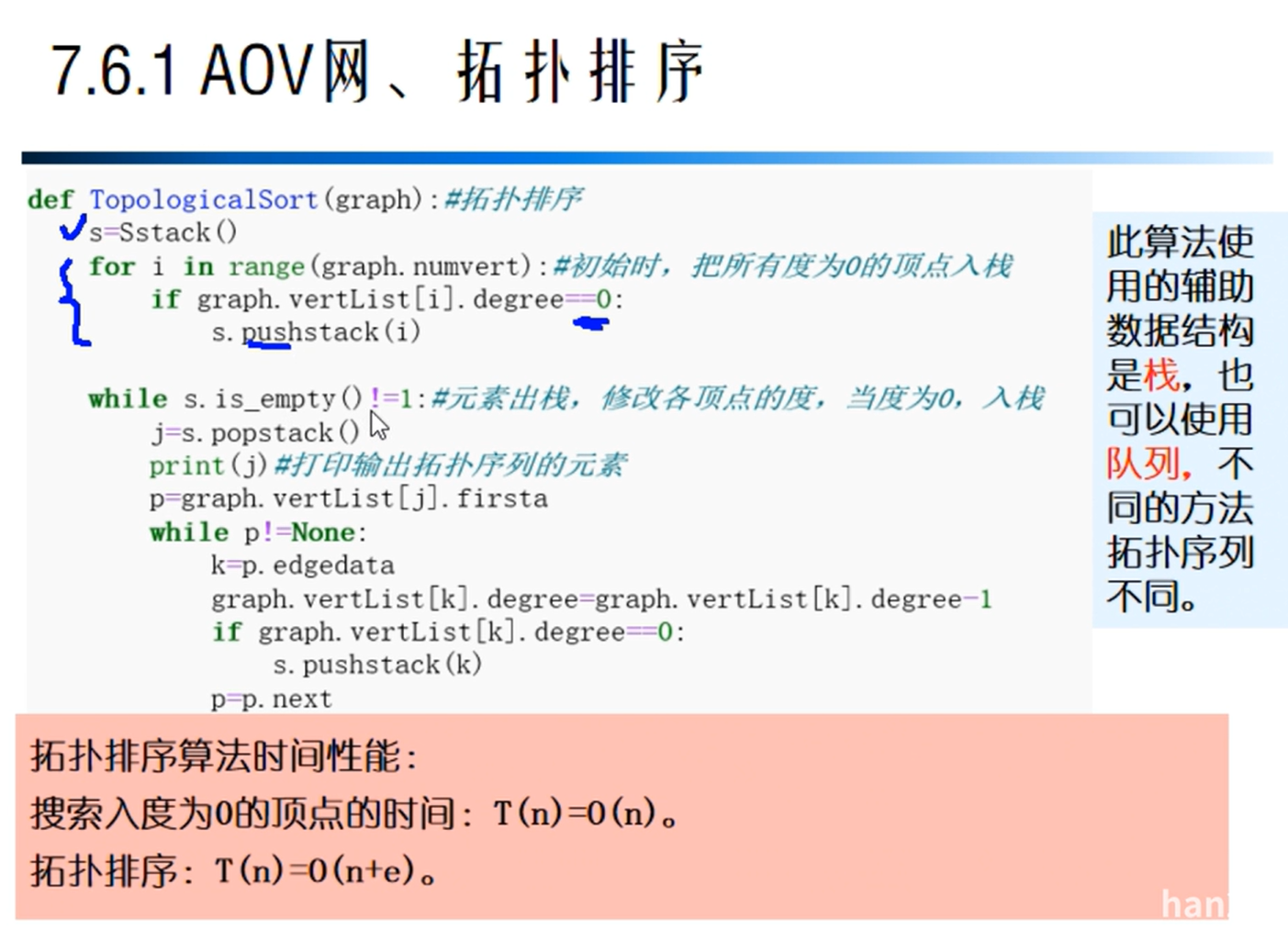
AOV网
拓扑排序
AOE网
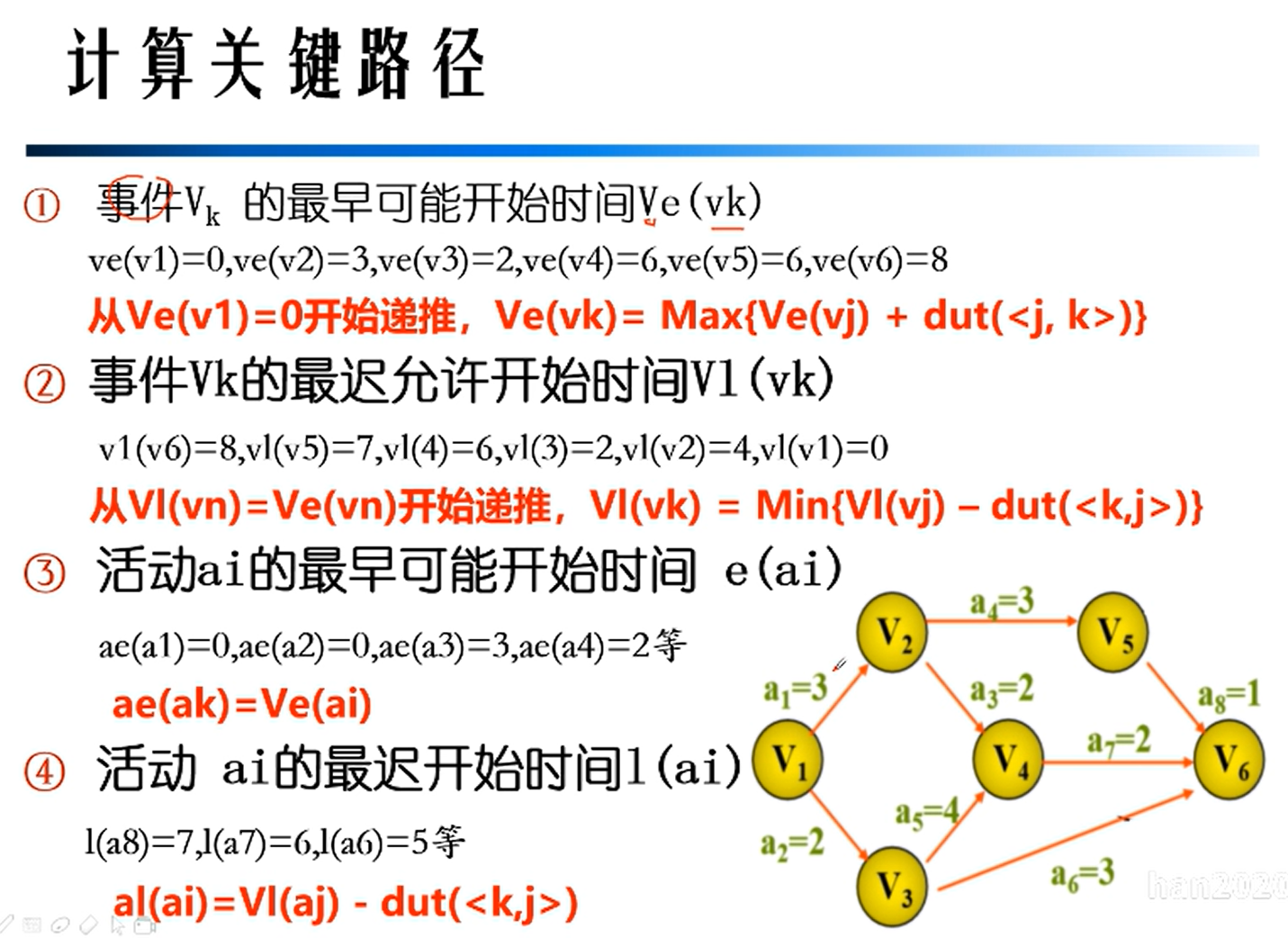
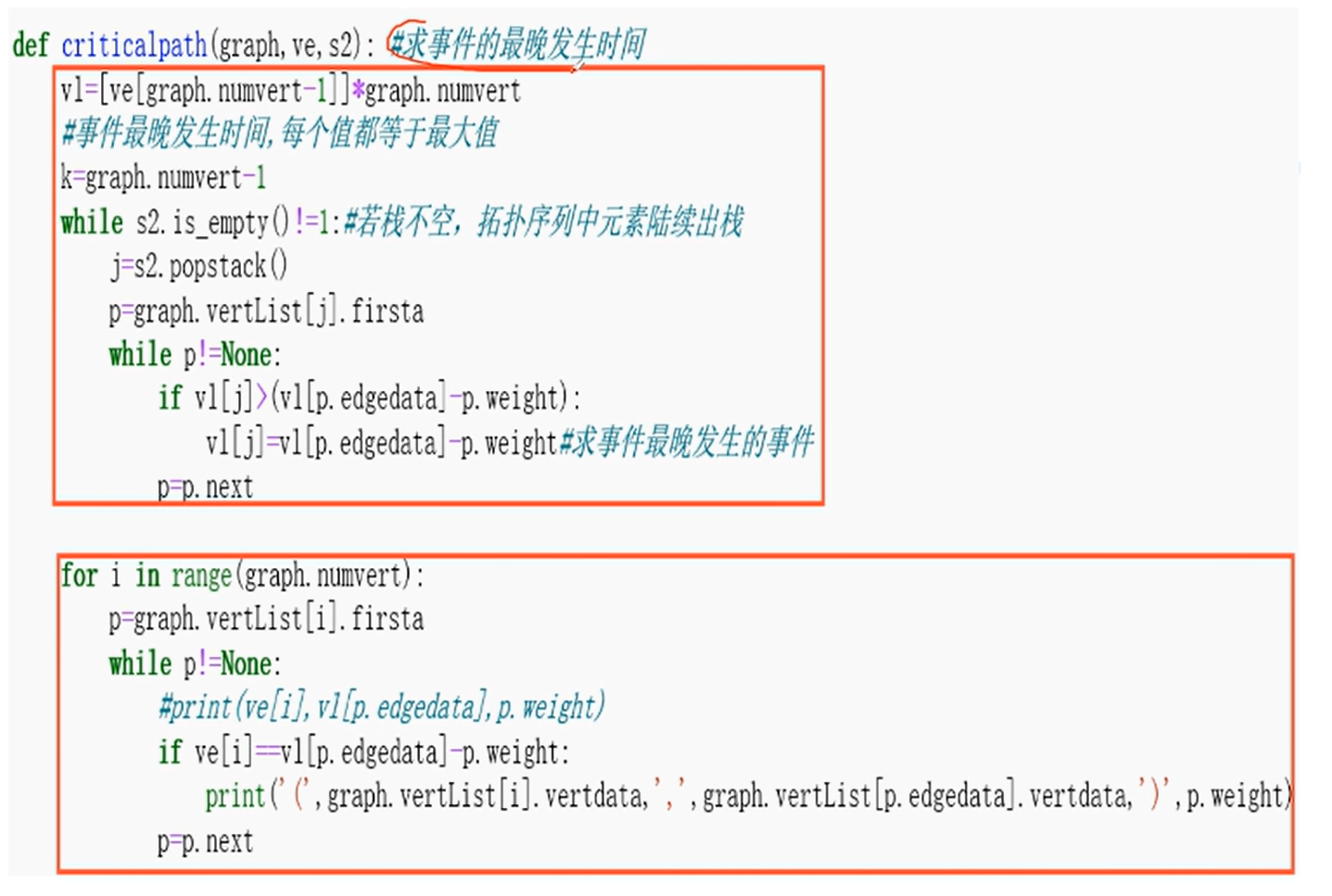
关键路径
贪心算法

找零问题

代码
1 | t = [100, 50, 20, 5, 1] |
分数背包问题


代码
1 | goods=[(60,10),(100,20),(120,30)] |
拼接最大数字问题

代码
1 | from functools import cmp_to_key |
活动选择问题


代码
1 | from operator import itemgetter |
动态规划(DP算法)

钢管切割问题
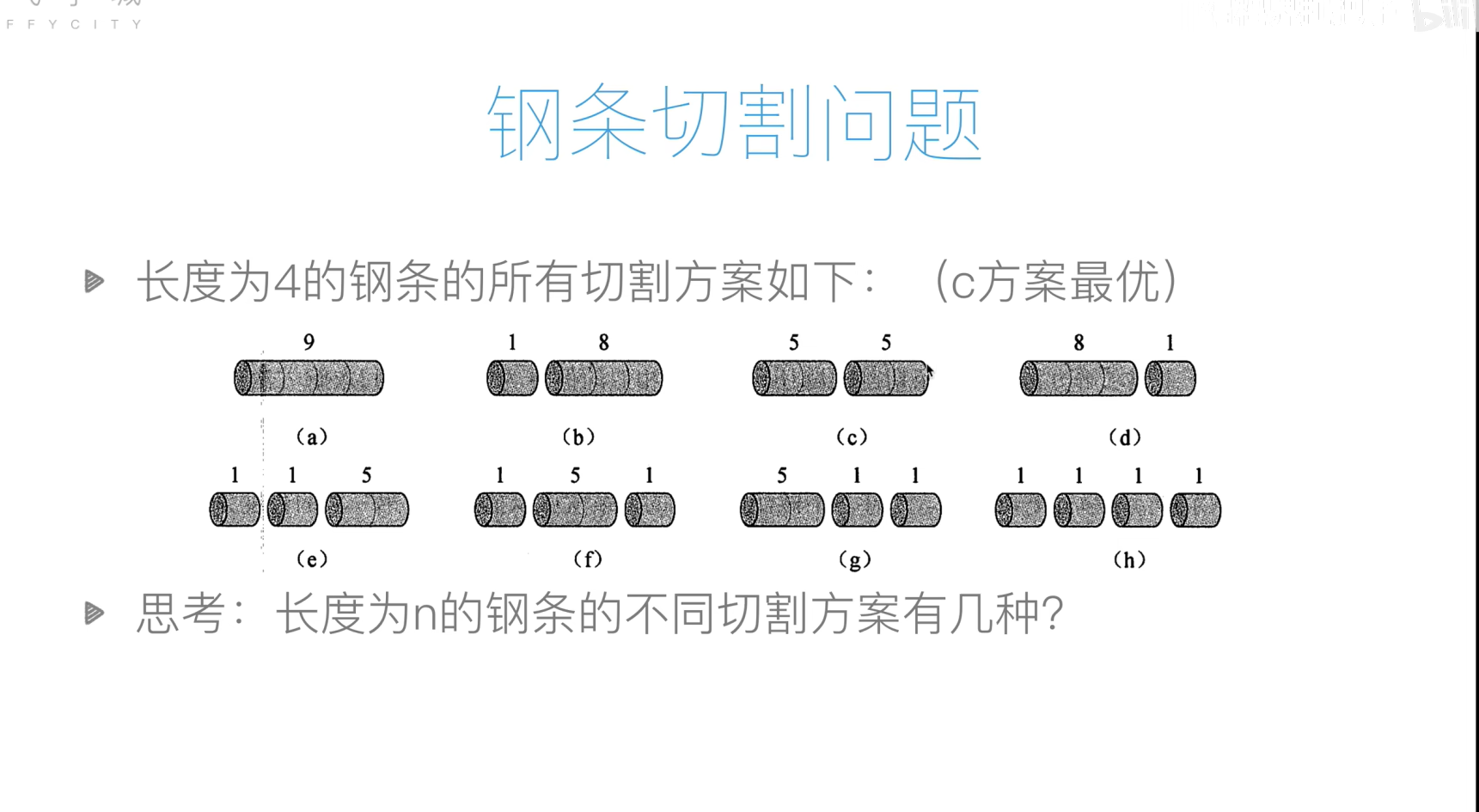
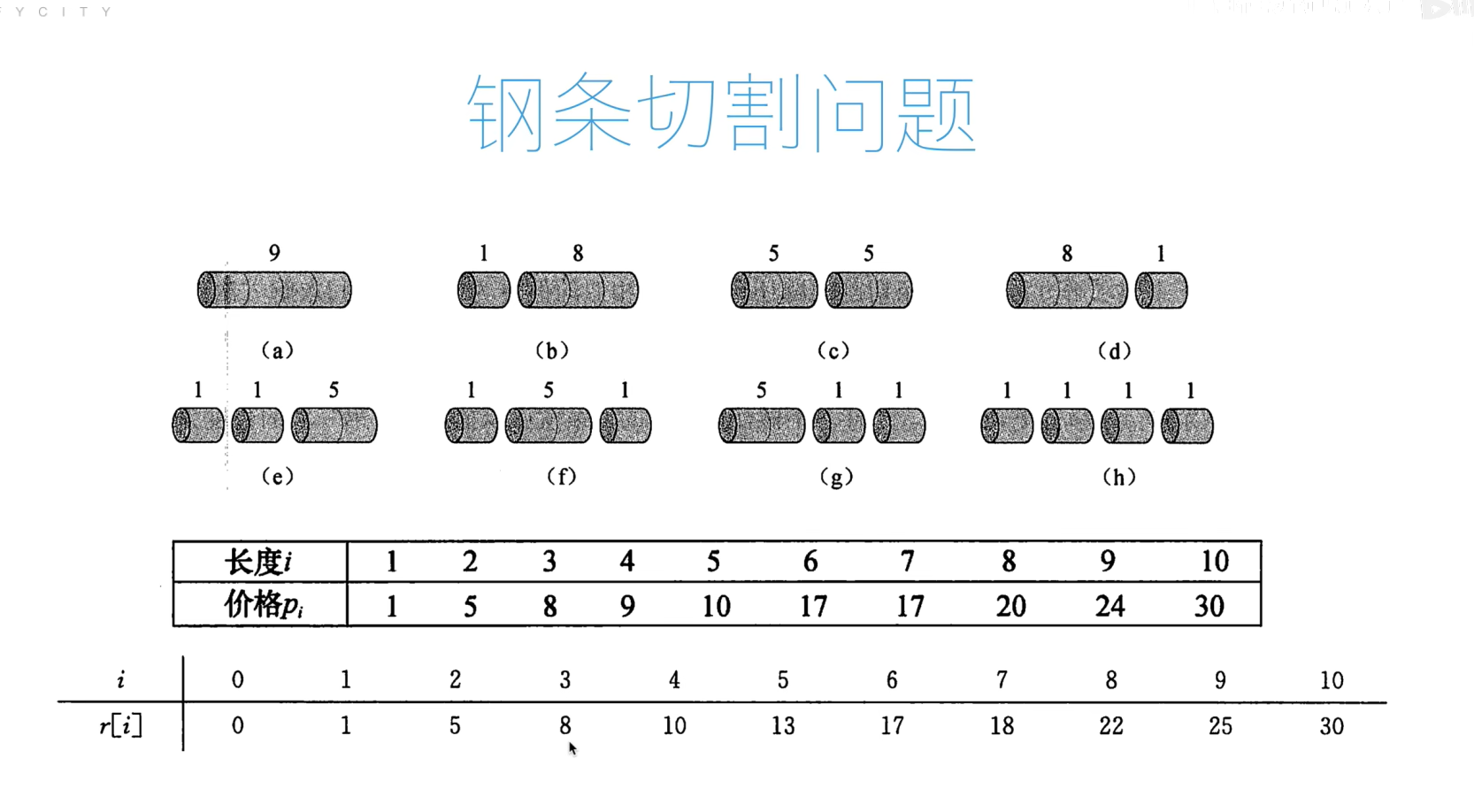




代码
1 | def cut_rot_dp(p, n): |
最长公共子序列问题


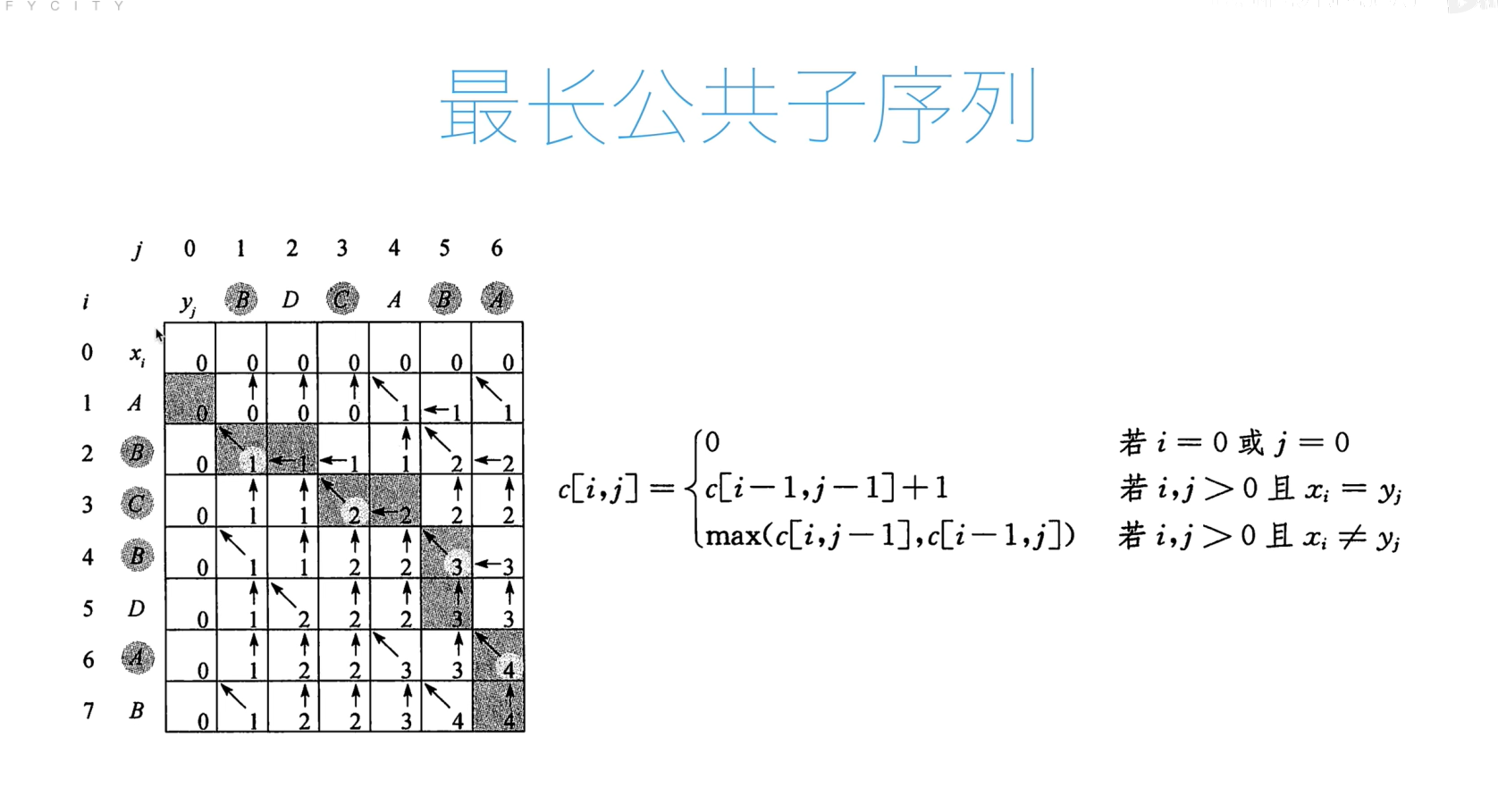
代码
1 | def lcs(x, y): |
欧几里得算法(求最大公约数)

1 | def gcd(a, b): |
应用

1 | class Fraction: |
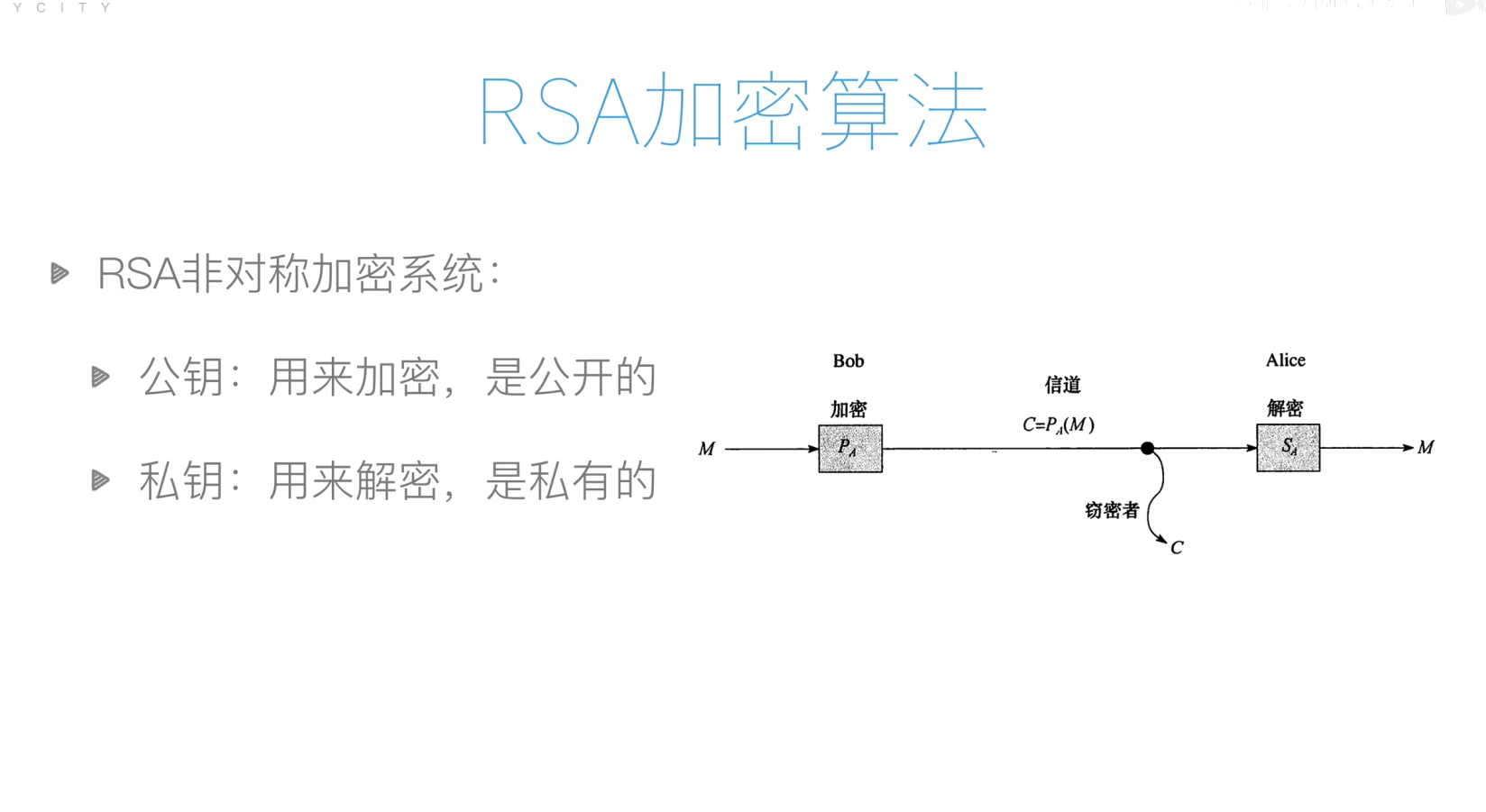
RSA加密算法



面向对象


设计模式




创建型模式
简单工厂模式


工厂方法模式


抽象工厂模式



建造者模式


单例模式


小结

结构型模式
适配器模式


桥模式



组合模式

外观模式


代理模式


行为型模式
责任链模式


观察者模式


模板方法模式


策略模式


本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 青墨染烟雨!
评论
WalineTwikoo